题目内容
已知函数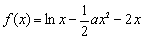 (
(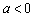 ).
).
(Ⅰ)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数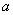 的取值范围;
的取值范围;
(Ⅱ)若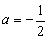 ,且关于
,且关于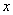 的方程
的方程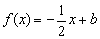 在
在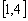 上恰有两个不等的实根,
上恰有两个不等的实根,
求实数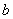 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列 满足
满足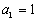 ,
,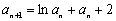 (
(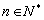 ),
),
求证: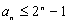 .
.
解:(Ⅰ)函数的定义域为 ,
,
 ,依题意
,依题意 在
在 时恒成立,
时恒成立,
则 在
在 时恒成立,即
时恒成立,即 ,
,
当 时,
时, 取最小值-1,所以
取最小值-1,所以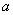 的取值范围是
的取值范围是
(Ⅱ) ,由
,由 得
得 在
在 上有两个不同的实根,
上有两个不同的实根,
设
 ,
, 时,
时, ,
, 时,
时,
 ,
, ,
,
 ,得
,得
则
(Ⅲ)易证当 且
且 时,
时, .
.
由已知条件 ,
,
故 所以当
所以当 时,
时,

 ,
, 相乘得
相乘得 又
又 故
故 ,即
,即

练习册系列答案
相关题目
 +
+ ≥μ恒成立的μ的取值范围是________.
≥μ恒成立的μ的取值范围是________. 的最小值为( )
的最小值为( )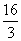 B.
B. C.
C.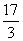 D.
D.
 的右焦点为
的右焦点为 ,过
,过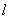 交双曲线的渐近线于A, B两点,且与其中一条渐近线垂直,若
交双曲线的渐近线于A, B两点,且与其中一条渐近线垂直,若 ,则该双曲线的离心率是
,则该双曲线的离心率是 (B)
(B) (C)
(C) (D)
(D) 
 中,对任意的正整数
中,对任意的正整数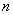 ,都有
,都有 ,且对任意的正整数
,且对任意的正整数 ,该数列中恰有
,该数列中恰有 个
个 = .
= .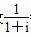 =________.
=________. ______.
______.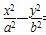 =1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为________.
=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为________.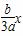 与双曲线
与双曲线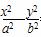 =1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.
=1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=________.