题目内容
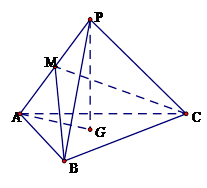
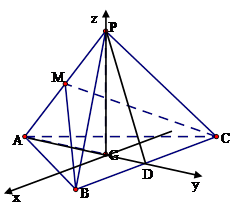
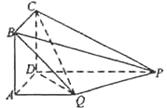
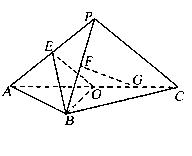
如图,三棱锥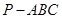 中,
中,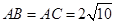 ,
, ,
,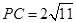 ,点
,点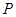 在平面
在平面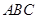 内的射影恰为
内的射影恰为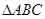 的重心
的重心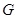 ,M为侧棱
,M为侧棱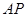 上一动点.
上一动点.
(1)求证:平面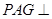 平面
平面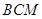 ;
;
(2)当M为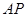 的中点时,求直线
的中点时,求直线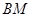 与平面
与平面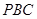 所成角的正弦值.
所成角的正弦值.
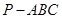 中,
中,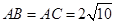 ,
, ,
,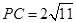 ,点
,点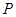 在平面
在平面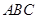 内的射影恰为
内的射影恰为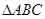 的重心
的重心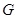 ,M为侧棱
,M为侧棱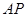 上一动点.
上一动点.
(1)求证:平面
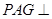 平面
平面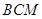 ;
;(2)当M为
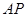 的中点时,求直线
的中点时,求直线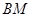 与平面
与平面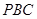 所成角的正弦值.
所成角的正弦值.(1)详见解析;(2)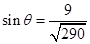 .
.
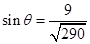 .
.试题分析:(1)证明平面
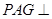 平面
平面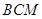 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面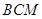 内找一条直线与平面
内找一条直线与平面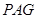 垂直,由已知
垂直,由已知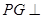 平面
平面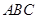 ,可得
,可得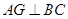 ,由题意可知,
,由题意可知,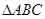 是等腰三角形,且
是等腰三角形,且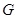 为重心,既得
为重心,既得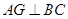 ,从而得
,从而得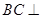 平面
平面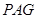 ,可证平面
,可证平面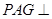 平面
平面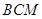 ;(2)当M为
;(2)当M为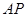 的中点时,求直线
的中点时,求直线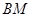 与平面
与平面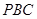 所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过
所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过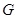 作
作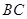 的平行线为
的平行线为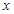 轴,
轴,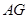 为
为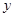 轴,
轴, 为
为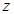 轴建立空间直角坐标系,写出各点的坐标,求出平面
轴建立空间直角坐标系,写出各点的坐标,求出平面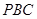 的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线
的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线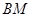 与平面
与平面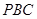 所成角的正弦值.
所成角的正弦值.试题解析:(1)取
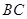 中点
中点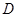 ,连接
,连接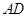 、
、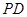 ,
,∵
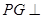 平面
平面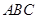 ,∴
,∴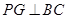
等腰
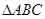 中,
中,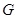 为重心,∴
为重心,∴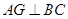
∴
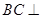 平面
平面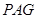
∴平面
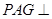 平面
平面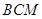 6分
6分(2)
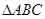 中,
中, ∴
∴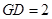
∵
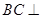 平面
平面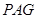 ∴
∴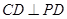
∴
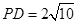 ∴
∴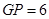
过
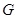 作
作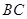 的平行线为
的平行线为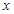 轴,
轴,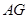 为
为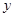 轴,
轴, 为
为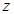 轴
轴建立空间直角坐标系
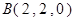
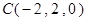
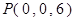
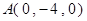
∴

设直线
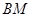 与平面
与平面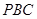 所成角为
所成角为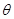
设平面
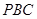 的法向量为
的法向量为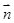
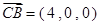
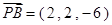 ∴
∴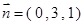
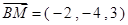 ∴
∴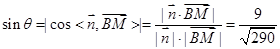 12分
12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
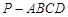 中,
中, 平面
平面 ,
, ,且
,且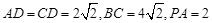 ,点
,点 在
在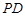 上.
上.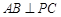 ;
;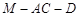 的大小为
的大小为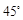 ,求
,求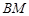 与平面
与平面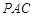 所成角的正弦值.
所成角的正弦值.
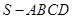 的底面是正方形,侧棱
的底面是正方形,侧棱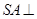 底面
底面 ,过
,过 作
作 垂直
垂直 交
交 点,作
点,作 垂直
垂直 交
交 点,平面
点,平面 交
交 于
于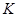 点,且
点,且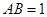 ,
,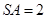 .
.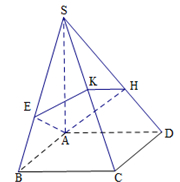
 是
是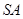 上任一点,试求
上任一点,试求 的最小值;
的最小值; 为直径的圆上;
为直径的圆上;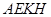 与平面
与平面 中,底面
中,底面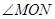 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的点.
上的点.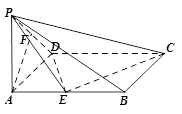
 是
是 的中点时,求证:
的中点时,求证: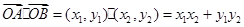 平面
平面 ;
;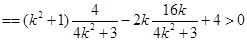 的大小为
的大小为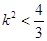 ,试确定
,试确定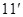 点的位置.
点的位置.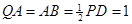 .
.
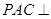 平面
平面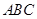 ,
,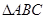 是以
是以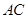 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,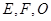 分别为
分别为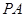 ,
,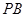 ,
,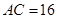 ,
,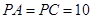 .
.
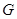 是
是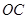 的中点,证明:
的中点,证明: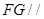 平面
平面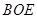 ;
;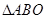 内存在一点
内存在一点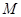 ,使
,使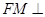 平面
平面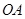 ,
,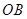 的距离.
的距离.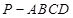 中,
中,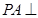 面
面 ,
,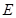 、
、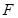 分别为
分别为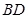 、
、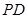 的中点,
的中点,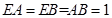 ,
,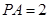 .
.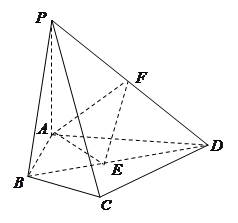
 ∥面
∥面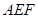 ;
;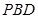 与面
与面 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.