题目内容
已知点A(1,0),B(0,1)和互不相同的点P1,P2,P3,…,Pn,…,满足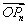 =an
=an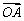 +bn
+bn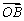 (n∈N*),其中{an},{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
(n∈N*),其中{an},{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
(1)求a1,b1的值.
(2)点P1,P2,P3,…,Pn,…能否在同一条直线上?请证明你的结论.
解:(1)P1是线段AB的中点⇒ =
=
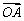 +
+
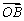 ,
,
又 =a1
=a1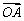 +b1
+b1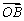 ,且
,且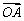 ,
,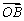 不共线,
不共线,
由平面向量基本定理,知a1=b1= .
.
(2)由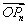 =an
=an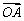 +bn
+bn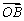 (n∈N*)⇒
(n∈N*)⇒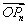 =(an,bn),
=(an,bn),
设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立.
若d=0,q≠1,则an=a1= (n∈N*)
(n∈N*)
⇒P1,P2,P3,…,Pn,…都在直线x= 上;
上;
若q=1,d≠0,则bn= 为常数列
为常数列
⇒P1,P2,P3,…,Pn,…都在直线y= 上;
上;
若d≠0且q≠1,P1,P2,P3,…,Pn,…在同一条直线上⇔ =(an-an-1,bn-bn-1)与
=(an-an-1,bn-bn-1)与 =(an+1-an,bn+1-bn)始终共线(n≥2,n∈N*)
=(an+1-an,bn+1-bn)始终共线(n≥2,n∈N*)
⇔(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0
⇔d(bn+1-bn)-d(bn-bn-1)=0
⇔bn+1-bn=bn-bn-1
⇔q=1,这与q≠1矛盾,
所以当d≠0且q≠1时,P1,P2,P3,…,Pn,…不可能在同一条直线上.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1. 5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
那么方程 的一个最接近的近似根为( )
的一个最接近的近似根为( )
A. B.
B. C.
C. D.
D.

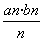 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn. :
: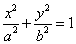 的离心率
的离心率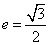 且与双曲线
且与双曲线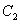 :
: 有共同焦点.
有共同焦点. ,求
,求 ,过椭圆
,过椭圆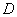 作
作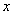 轴的垂线交
轴的垂线交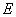 ,若
,若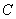 点满足
点满足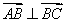 ,
,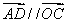 ,连结
,连结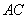 交
交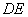 于点
于点 ,求证:
,求证: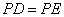 .
. ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.