题目内容
已知椭圆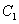 :
: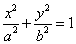 的离心率
的离心率
为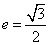 且与双曲线
且与双曲线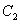 :
: 有共同焦点.
有共同焦点.
(1)求椭圆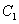 的方程;
的方程;
(2)在椭圆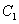 落在第一象限的图像上任取一点作
落在第一象限的图像上任取一点作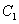 的切线
的切线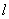 ,求
,求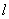 与坐标轴围成的三角形的面积的最小值;
与坐标轴围成的三角形的面积的最小值;
(3)设椭圆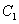 的左、右顶点分别为
的左、右顶点分别为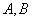 ,过椭圆
,过椭圆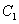 上的一点
上的一点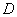 作
作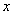 轴的垂线交
轴的垂线交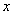 轴于点
轴于点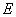 ,若
,若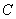 点满足
点满足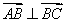 ,
,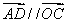 ,连结
,连结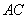 交
交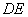 于点
于点 ,求证:
,求证: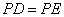 .
.
 (2)设直线
(2)设直线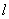 的方程为:
的方程为:
 ,代入椭圆
,代入椭圆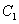 方程中,消去y,得到关于x的一元二次方程,其判别式等于零,可得
方程中,消去y,得到关于x的一元二次方程,其判别式等于零,可得 ,在求出直线l与坐标轴的交点,写出围成的三角形的面积
,在求出直线l与坐标轴的交点,写出围成的三角形的面积 ,再把
,再把 代入,即可最的最小值.
代入,即可最的最小值.


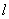 与坐标轴围成的三角形的面积
与坐标轴围成的三角形的面积 ⑤,
⑤,
④代入⑤可得: (当且仅当
(当且仅当 时取等号)
时取等号)
(3)由(1)得 ,设
,设 ,
,
 ,
, 可设
可设 ,
,

 3.
3.

练习册系列答案
相关题目
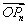 =an
=an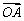 +bn
+bn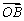 (n∈N*),其中{an},{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
(n∈N*),其中{an},{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点. ,
, ,且
,且 ,则向量
,则向量 与
与 夹角的大小为( )
夹角的大小为( ) B.
B.  C.
C. D.
D.
 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( ) B.
B. C.
C. D.
D.
 在区间
在区间 内
内 个零点 C.有且仅有
个零点 C.有且仅有 个零点 D.有且仅有
个零点 D.有且仅有 个零点
个零点 >
> -
- ;
;