题目内容
4.现有5张卡片,其正反两面分别写有0与1、2与3、4与5、6与7、8与9,用这五涨卡片可以组成不同的四位数的个数为4536.分析 根据分步计数原理即可求出.
解答 解:首先抽确定千位,有9个选择(千位不能是0),第二步确定百位,有9种选择(可以选择0了),第三步确定十位,有8种选择,第四步确定个位,有7种选择
所以根据乘法原理,总共有9×9×8×7=4536种选择,
故答案为:4536
点评 本题考查了分步计数原理,关键是分步,并注意首位不能为0,属于基础题.

练习册系列答案
相关题目
13.已知等比数列{an}的首项为1,若4a1,2a2,a3成等差数列,数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,则满足不等式Sn>$\frac{125}{63}$的n的最小值为( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
12.若集合M={1,2,3,4},N={x|x(x-3)<0},则M∩N等于( )
| A. | {1,2,3} | B. | {1,2} | C. | {x|1<x<3} | D. | {2,3,4} |



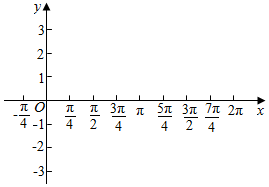 已知函数f(x)=3sin(x+$\frac{π}{4}$).
已知函数f(x)=3sin(x+$\frac{π}{4}$).