题目内容
16. 已知函数f(x)=3sin(x+$\frac{π}{4}$).
已知函数f(x)=3sin(x+$\frac{π}{4}$).(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)写出f(x)的值域、最小正周期、对称轴,单调区间.
分析 (1)根据函数f(x)的解析式,先列表,后描点并画出f(x)在一个周期上的图象;
(2)根据函数f(x)的图象,写出f(x)的值域、最小正周期、对称轴与单调增区间和单调减区间.
解答 解:(1)函数f(x)=3sin(x+$\frac{π}{4}$),先列表,
| x | -$\frac{π}{4}$ | $\frac{π}{4}$ | $\frac{3π}{4}$ | $\frac{5π}{4}$ | $\frac{7π}{4}$ |
| x+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sin(x+$\frac{π}{4}$) | 0 | 1 | 0 | -1 | 0 |
| y | 0 | 3 | 0 | -3 | 0 |
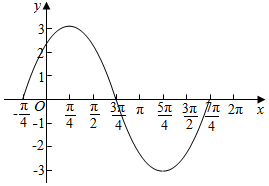
(2)根据函数f(x)的图象得,
f(x)的值域是[-3,3],最小正周期为T=2π,
对称轴为x=$\frac{π}{4}$+kπ,k∈Z;
单调增区间为[-$\frac{3π}{4}$+2kπ,$\frac{π}{4}$+2kπ],k∈Z,
单调减区间为[$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ],k∈Z.
点评 本题考查了正弦函数的画法,五点作图法问题,先列表,再画图是做好本题的基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目