题目内容
17.已知a,b,c分别为△ABC三个内角A,B,C的对边,$bcosA+\sqrt{3}bsinA-c-a=0$.(1)求角B的大小;
(2)若$b=\sqrt{3}$,求a+c的最大值.
分析 (1)由正弦定理化简已知的等式,由内角和定理、诱导公式、两角和差的正弦公式化简后,由内角的范围和特殊角的三角函数值求出B;
(2)由(1)和余弦定理列出方程化简后,利用完全平方公式和基本不等式求出a+c的最大值.
解答 解:(1)由题意得,$bcosA+\sqrt{3}bsinA-c-a=0$,
由正弦定理得,$sinBcosA+\sqrt{3}sinBsinA-sinC-sinA=0$,
所以$sinBcosA+\sqrt{3}sinBsinA-sin({A+B})-sinA=0$,
则$sinBcosA+\sqrt{3}sinBsinA-sinAcosB-cosAsinB-sinA=0$,
化简得,$\sqrt{3}sinBsinA-sinAcosB-sinA=0$,
又sinA≠0,则$\sqrt{3}sinB-cosB=1$,…(4分),
即$sin({B-\frac{π}{6}})=\frac{1}{2}$,
由于B∈(0,π),所以$B=\frac{π}{3}$…(7分)
(2)由(1)和余弦定理得,b2=a2+c2-2accosB…(9分),
又b=$\sqrt{3}$,化简得a2+c2-ac=3…(11分),
所以${({a+c})^2}=3+3ac≤3+3{({\frac{a+c}{2}})^2}$,
解得a+c≤$2\sqrt{3}$,当且仅当a=c取等号…(14分)
所以当$a=c=\sqrt{3}$时,a+c的最大值为$2\sqrt{3}$.…(15分)
点评 本题考查了正弦定理、余弦定理,内角和定理、诱导公式、两角和差的正弦公式,以及基本不等式在求最值中的应用,考查化简、变形能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若x轴为曲线f(x)=x3-ax-$\frac{1}{4}$的切线,则a=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,则a-b=( )
| A. | -7 | B. | -2 | C. | -7和-2 | D. | 以上答案都不对 |
9.若α为第三象限角,则$\sqrt{1-sin{α}^{2}}$的结果为( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
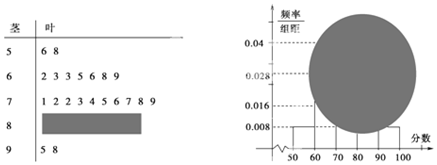
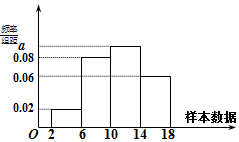 如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:
如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题: