题目内容
8.已知f(x)=|x+2|+|x-1|.(1)求不等式f(x)>5的解集;
(2)若f(x)≥a2-2a恒成立,求实数a的取值范围.
分析 (1)问题转化为解不等式组问题,求出不等式的解集即可;
(2)要使f(x)≥|a-1|对任意实数x∈R成立,得到|a-1|≤3,解出即可.
解答 解:(1)不等式f(x)>5即为|x+2|+|x-1|>5,
等价于$\left\{\begin{array}{l}{x<-2}\\{-x-2-x+1>5}\end{array}\right.$或 $\left\{\begin{array}{l}{-2≤x≤1}\\{x+2-x+1>5}\end{array}\right.$或 $\left\{\begin{array}{l}{x>1}\\{x+2+x-1>5}\end{array}\right.$,
解得x<-3或x>2,
因此,原不等式的解集为{x|x<-3或x>2};
(2)f(x)=|x+2|+|x-1|≥|x+2-x+1|=3,
若f(x)≥a2-2a恒成立,则a2-2a-3≤0,
则(a-3)(a+1)≤0,解得:-1≤a≤3.
点评 本题考查了绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
16.复数$z=\frac{{3-2{i^2}}}{1+i}$的虚部为( )
| A. | $-\frac{5}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
3.用秦九韶算法求多项式f(x)=x6+6x4+9x2+208在x=-4时,v2的值为( )
| A. | -4 | B. | 1 | C. | 17 | D. | 22 |
13.函数y=f(x)在点(x0,y0)处的切线方程为y=2x+1,则$\lim_{△x→0}\frac{{f({x_0})-f({{x_0}-△x})}}{△x}$=( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
17.在△ABC中,a,b,c分别为A,B,C的对边,已知a,b,c成等比数列,a2-c2=ac+bc,a=3$\sqrt{3}$,则$\frac{b+c}{sinB+sinC}$=( )
| A. | 12 | B. | 6$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 6 |
 如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.
如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.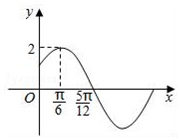 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)