题目内容
【题目】如图,几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,面
,面![]() ∥面
∥面![]() ,
,![]() 、
、![]() 、
、![]() 都垂直于面
都垂直于面![]() ,且
,且![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() 为等腰直角三角形;
为等腰直角三角形;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)详见解析;(2) ![]() .
.
【解析】
试题分析:(1)由已知条件,在直角三角形![]() ,DCE中分别求出
,DCE中分别求出![]() ,DE的长度,由边的关系能够证出△DB1E为等腰直角三角形;(2)取
,DE的长度,由边的关系能够证出△DB1E为等腰直角三角形;(2)取![]() 的中点H,因为O,H分别为DB,
的中点H,因为O,H分别为DB,![]() 的中点,所以OH∥BB1,以OA,OB,OH分别为x,y,z轴建立坐标系,求出两个平面
的中点,所以OH∥BB1,以OA,OB,OH分别为x,y,z轴建立坐标系,求出两个平面![]() 和DFE的法向量,根据二面角与其法向量所成角的关系求二面角
和DFE的法向量,根据二面角与其法向量所成角的关系求二面角![]() 的余弦值.
的余弦值.
试题解析:解:(1)连接![]() ,交
,交![]() 于
于![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形,![]() ,所以
,所以![]()
因为![]() 、
、![]() 都垂直于面
都垂直于面![]() ,
,![]()
![]() ,又面
,又面![]() ∥面
∥面![]() ,
,![]()
所以四边形![]() 为平行四边形 ,则
为平行四边形 ,则![]() 2分
2分
因为![]() 、
、![]() 、
、![]() 都垂直于面
都垂直于面![]() ,则
,则![]()
![]()
![]() 4分
4分
所以![]()
所以![]() 为等腰直角三角形 5分
为等腰直角三角形 5分
(2)取![]() 的中点
的中点![]() ,因为
,因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ∥
∥![]()
以![]() 分别为
分别为![]() 轴建立坐标系,
轴建立坐标系,
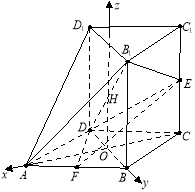
则![]()
所以![]() 7分
7分
设面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即![]() 且
且![]()
令![]() ,则
,则![]() 9分
9分
设面![]() 的法向量为
的法向量为,
则![]() 即
即![]() 且
且![]()
令![]() ,则
,则![]() 11分
11分
则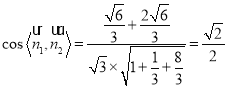 ,则二面角
,则二面角![]() 的余弦值为
的余弦值为![]() 12分
12分

练习册系列答案
相关题目