题目内容
18.已知a1+2a2+3a3+…+nan=$\frac{1}{4}$[(2n-1)an+1+1],a1=1,则an=3n-1.分析 化简可得(n+1)an+1=$\frac{1}{4}$[(2n+1)an+2+1]-$\frac{1}{4}$[(2n-1)an+1+1],从而可判断数列{an}是以1为首项,3为公比的等比数列,从而解得.
解答 解:∵a1+2a2+3a3+…+nan=$\frac{1}{4}$[(2n-1)an+1+1],
a1+2a2+3a3+…+nan+(n+1)an+1=$\frac{1}{4}$[(2n+1)an+2+1],
两式作差可得,
(n+1)an+1=$\frac{1}{4}$[(2n+1)an+2+1]-$\frac{1}{4}$[(2n-1)an+1+1],
化简可得,an+2=3an+1,
当n=1时,a1=$\frac{1}{4}$(a2+1),解得,a2=3;
故数列{an}是以1为首项,3为公比的等比数列,
故an=1•3n-1=3n-1,
故答案为:3n-1.
点评 本题考查了数学归纳法的应用及分类讨论的思想应用,同时考查了等比数列的性质应用.

练习册系列答案
相关题目
8.执行如图所示的程序框图,输出S的值是( )
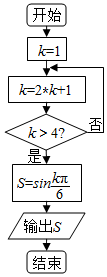

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
6.执行如图的程序框图,若输入M的值为1,则输出的S=( )


| A. | 6 | B. | 12 | C. | 14 | D. | 20 |
13.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2},}}&{x≤0}\\{1+x{e}^{x-1},}&{x>0}\end{array}\right.$,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
| A. | (0,$\frac{π}{4}$) | B. | (0,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$) | D. | (0,$\frac{π}{3}$] |
 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.