题目内容
9.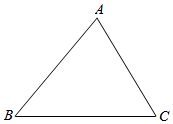 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.
分析 利用正弦定理把b,c用B,C表示出来,根据C=$\frac{2π}{3}-B$将L表示成关于B的函数,利用B的范围求出L的最大值.
解答 解:由正弦定理得$\frac{c}{sinC}=\frac{b}{sinB}=\frac{a}{sinA}=2\sqrt{3}$.
∴b=2$\sqrt{3}$sinB,c=2$\sqrt{3}$sinC=2$\sqrt{3}$sin($\frac{2π}{3}-B$)=3cosB+$\sqrt{3}$sinB.
∴L=a+b+c=3+3$\sqrt{3}$sinB+3cosC=3+6sin(B+$\frac{π}{6}$).
∵0<B<$\frac{2π}{3}$,
∴当B=$\frac{π}{3}$时,L取得最大值9.
点评 本题考查了正弦定理,三角函数的恒等变换,正弦函数的性质,属于中档题.

练习册系列答案
相关题目
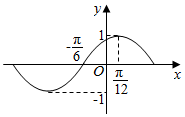
20.函数f(x)=cos(ωx+φ)的部分图象如图所示,则下列结论成立的是( )

| A. | f(x)的递增区间是(2kπ-$\frac{5π}{12}$,2kπ+$\frac{π}{12}$),k∈Z | |
| B. | 函数f(x-$\frac{π}{3}$)是奇函数 | |
| C. | 函数f(x-$\frac{π}{12}$)是偶函数 | |
| D. | f(x)=cos(2x-$\frac{π}{6}$) |
17.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{3}x|\\;0<x<3}\\{sin(\frac{π}{6}x)\\;3≤x≤15}\end{array}\right.$,若存在实数x1,x2,x3,x4满足f(x1)=f(x2)=f(x3)=f(x4),其中x1<x2<x3<x4,则x1x2x3x4取值范围是( )
| A. | (60,96) | B. | (45,72) | C. | (30,48) | D. | (15,24) |
1.在长为2的线段AB上任意取一点C,以线段AC为半径的圆面积小于π的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{π}{4}$ |
19.已知关于x的方程x2-(5+i)x+4+ai=0(a∈R)有实数根b,则|a+bi|等于( )
| A. | $\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{2}$或4$\sqrt{2}$ | D. | 5 |