题目内容
1.在△ABC中,AB=$\sqrt{3}$,AC=1,∠B=30°,△ABC的面积为$\frac{{\sqrt{3}}}{4}$,则∠C=( )| A. | 30° | B. | 120° | C. | 60° | D. | 45° |
分析 利用已知及三角形面积公式可求BC,利用余弦定理即可求得cosC的值,结合C的范围即可得解.
解答 解:在△ABC中,∵AB=$\sqrt{3}$,AC=1,∠B=30°,
∴△ABC的面积为$\frac{\sqrt{3}}{4}$=$\frac{1}{2}$AB•BC•sinB=$\frac{1}{2}$×$\sqrt{3}$×BC×$\frac{1}{2}$,解得:BC=1,
∴由余弦定理可得:cosC=$\frac{{AC}^{2}{+BC}^{2}{-AB}^{2}}{2AC•BC}$=$\frac{1+1-3}{2×1×1}$=-$\frac{1}{2}$,
∵C∈(0,180°),
∴C=120°.
故选:B.
点评 本题主要考查了三角形面积公式,余弦定理的综合应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设△ABC的内角A,B,C所对的边分别为a,b,c,且b2=a2+c2+2accosB,则∠B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
16.在△ABC中,已知c=$\sqrt{6}$,A=$\frac{π}{4}$,a=2,则角C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{12}$或$\frac{5π}{12}$ |
13.已知等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a7=( )
| A. | 18 | B. | 24 | C. | 30 | D. | 42 |
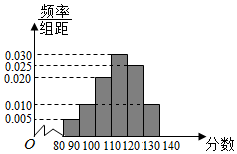 2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.
2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.