题目内容
已知函数y=
的值域为[0，+∞），则a的取值范围是 ．
| x2+2ax+3+2a |
考点：函数的值域
专题：函数的性质及应用
分析：既然函数的值域是[0，+∞），则函数f（x）=x2+2ax+3+2a的函数值取遍所有的正实数，所以函数f（x）的图象与x轴相交或相切，因此△≥0，列出a的不等式解出s即为所求．
解答：
解：由题意函数y=
的值域为[0，+∞），
∴f（x）=x2+2ax+3+2a的函数值取遍所有的正实数，又该函数图象开口向上，
∴只需f（x）=x2+2ax+3+2a对应方程得判别式△=（2a）2-4（3+2a）≥0，
即a2-2a-3≥0，
解得a≤-1或a≥3．
故答案为：（-∞，-1]∪[3，+∞）
| x2+2ax+3+2a |
∴f（x）=x2+2ax+3+2a的函数值取遍所有的正实数，又该函数图象开口向上，
∴只需f（x）=x2+2ax+3+2a对应方程得判别式△=（2a）2-4（3+2a）≥0，
即a2-2a-3≥0，
解得a≤-1或a≥3．
故答案为：（-∞，-1]∪[3，+∞）
点评：这个题的关键是函数f（x）=x2+2ax+3+2a的函数值能够取遍所有的正实数，而非x2+2ax+3+2a≥0恒成立，借助于二次函数的图象可知，当该二次函数图象与x轴相切或相交时才能满足题意，所以判别式△≥0，解出a的值求解．
练习册系列答案
相关题目
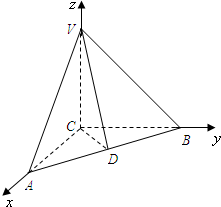如图，在三棱锥V-ABC中，顶点C在空间直角坐标系的原点处，顶点A、B、V分别在x、y、z轴上，D是AB的中点，且AC=BC=2，∠VDC=θ．