Question

【题目】（本小题满分14分）

已知数列是首项为1，公比为2的等比数列，数列的前项和．

（1）求数列与的通项公式；

（2）求数列的前项和．

Answer 1

【答案】解：（1）因为数列是首项为1，公比为2的等比数列，

所以数列的通项公式为．………………………………………………2分

因为数列的前项和．

所以当时，，

当时，，

所以数列的通项公式为．………………………………………………6分

（2）由（1）可知，．……………………………………………………7分

设数列的前项和为，

则， ①……………9分

即， ②……………10分

①－②，得……………………………11分

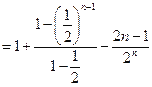
，………………………………………………………13分

所以．

故数列的前项和为．………………………………………………14分

【解析】试题（1）数列的前项和当时 ， 所以数列的通项公式为（2）由则

两式相减得

试题解析：（1）因为数列是首项为1，公比为2的等比数列，

所以数列的通项公式为． （3分）

因为数列的前项和．

所以当时， ，

当时， ，

所以数列的通项公式为． （6分）

（2）由（1）可知， ．

设数列的前项和为，

则， ①

即， ②

①－②，得

，

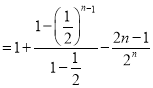
所以．

故数列的前项和为． （12分）