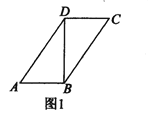
题目内容
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以对角线
,以对角线![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到图2所示点
到图2所示点![]() 的位置,使得
的位置,使得![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)在图1中,求解三角形可得AB⊥BD,同理CD⊥BD,图2中,在△PAD中,求解三角形可得AD⊥PD,结合PD⊥BD,得到PD⊥平面ABD,进一步得到PD⊥AB,
又AB⊥BD,可得AB⊥平面PBD,由面面垂直的判定可得平面PAB⊥平面PBD;
(Ⅱ)以D为坐标原点,分别以DB,DP所在直线为y,z轴,过点D在平面ABD内平行于AB的直线为x轴建立空间直角坐标系,分别求出平面PAD与平面PAB的一个法向量,由两法向量所成角的余弦值可得二面角B-PA-D的余弦值.
(Ⅰ)图1中,![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即![]() ,
,
同理![]() .
.
图2中,在![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
又![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() .∴
.∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,
过点![]() 在平面
在平面![]() 内平行于
内平行于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
由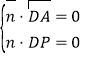 得
得![]() 令
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]()
同理可得平面![]() 的一个法向量
的一个法向量![]()
∴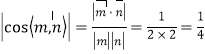 .
.
又二面角![]() 的平面角为锐角,
的平面角为锐角,
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目