Question

【题目】已知椭圆，点在椭圆上，椭圆的离心率是.

（1）求椭圆的标准方程；

（2）设点为椭圆长轴的左端点，为椭圆上异于椭圆长轴端点的两点，记直线斜率分别为，若，请判断直线是否过定点？若过定点，求该定点坐标，若不过定点，请说明理由.

Answer 1

【答案】（1）（2）过定点

【解析】

（1）由点M（﹣1，）在椭圆C上，且椭圆C的离心率是，列方程组求出a＝2，b，由此能求出椭圆C的标准方程．

（2）设点P，Q的坐标分别为（x1，y1），（x2，y2），当直线PQ的斜率存在时，设直线PQ的方程为y＝kx+m，联立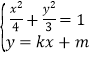，得：（4k2+3）x2+8kmx+（4m2﹣12）＝0，利用根的判别式、韦达定理，结合已知条件得直线PQ的方程过定点（1，0）；再验证直线PQ的斜率不存在时，同样推导出x0＝1，从而直线PQ过（1，0）．由此能求出直线PQ过定点（1，0）．

（1）由点在椭圆上，且椭圆的离心率是，

可得，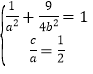

可解得：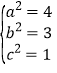

故椭圆的标准方程为.

（2）设点的坐标分别为，

（ⅰ）当直线斜率不存在时，由题意知，直线方程和曲线方程联立得：，，

（ⅱ）当直线的斜率存在时，设直线的方程为，

联立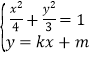，消去得：，

由，有，

由韦达定理得：，，

故，可得：，

可得：，

整理为：，

故有，

化简整理得：，解得：或，

当时直线的方程为，即，过定点不合题意，

当时直线的方程为，即，过定点，

综上，由（ⅰ）（ⅱ）知，直线过定点.