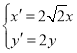题目内容
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上一动点,线段
上一动点,线段![]() 与圆
与圆![]() :
:![]() 相交于点
相交于点![]() .直线
.直线![]() 经过
经过![]() ,并且垂直于
,并且垂直于![]() 轴,
轴,![]() 在
在![]() 上的射影点为
上的射影点为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴的左、右交点分别为
轴的左、右交点分别为![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 上的点(点
上的点(点![]() 与
与![]() ,
,![]() 不重合),直线
不重合),直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别相交于点
分别相交于点![]() ,
,![]() ,求证:以
,求证:以![]() 直径的圆经过定点.
直径的圆经过定点.
【答案】(1)![]() (2)见证明
(2)见证明
【解析】
(1)设点![]() ,
,![]() ,由已知条件找到两点坐标之间的关系,然后利用相关点法即可求得点E的轨迹方程;(2)根据已知条件设直线AP,BP的方程,当x=4时可得点M,N的坐标,从而可得以MN为直径的圆的方程,整理即得圆经过的定点.
,由已知条件找到两点坐标之间的关系,然后利用相关点法即可求得点E的轨迹方程;(2)根据已知条件设直线AP,BP的方程,当x=4时可得点M,N的坐标,从而可得以MN为直径的圆的方程,整理即得圆经过的定点.
(1)设点![]() ,
,![]() .
.
当![]() 时,易得
时,易得![]() ;
;
当![]() 时,有
时,有![]() ,所以
,所以![]() .又
.又![]() ,所以
,所以![]() .
.
代入![]() 的方程,得
的方程,得![]() ,即
,即![]() .
.
(2)证明:设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,记
,记![]() .
.
则![]()
![]() ,
,![]() .
.
直线![]() 的方程为
的方程为![]() ,所以
,所以![]() .
.
直线![]() 的方程为
的方程为![]() ,所以
,所以![]() .
.
以![]() 为直径的圆的方程为
为直径的圆的方程为![]() .
.
整理,得![]()
![]() .
.
令![]() 解得
解得![]() 或
或![]()
所以以![]() 为直径的圆过定点
为直径的圆过定点![]() ,
,![]() .
.

练习册系列答案
相关题目
【题目】某日A, B, C三个城市18个销售点的小麦价格如下表:
销售点序号 | 所属城市 | 小麦价格(元/吨) | 销售点序号 | 所属城市 | 小麦价格(元/吨) |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
(Ⅰ)求B市5个销售点小麦价格的中位数;
(Ⅱ)甲从B市的销售点中随机挑选一个购买1吨小麦,乙从C市的销售点中随机挑选一个购买1吨小麦,求甲花费的费用比乙高的概率;
(Ⅲ)如果一个城市的销售点小麦价格方差越大,则称其价格差异性越大.请你对A、B、C三个城市按照小麦价格差异性从大到小进行排序(只写出结果).