题目内容
4.已知Sn是数列{an}的前n项和,a1=1,a2=2,a3=3,数列{an+an+1+an+2}是公差为2的等差数列,则S24=( )| A. | 110 | B. | 216 | C. | 214 | D. | 218 |
分析 由题意可判数列隔2项取出的数构成2为公差的等差数列,由等差数列的求和公式可得.
解答 解:∵数列{an+an+1+an+2}是公差为2的等差数列,
∴an+3-an=an+1+an+2+an+3-(an+an+1+an+2)=2,
∴数列隔2项取出的数构成2为公差的等差数列,
∵a1=1,a2=2,a3=3,
∴S24=a1+a2+a3+…+a24=(a1+a4+a7+…+a22)+(a2+a5+a8+…+a23)+(a3+a6+a9+…+a24)
=(8×1+$\frac{8×7}{2}$×2)+(8×2+$\frac{8×7}{2}$×2)+(8×3+$\frac{8×7}{2}$×2)
=216.
故选:B.
点评 本题考查等差数列的求和公式,得出数列隔2项取出的数构成2为公差的等差数列是解决问题的关键,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.对于R上可导的函数f(x),若满足(x-1)•f′(x)≥0,则下列说法错误的是( )
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | f(x)在(-∞,0)上是减函数 | ||
| C. | 当x=1时,f(x)取得极小值 | D. | f(0)+f(2)≥2f(1) |
19.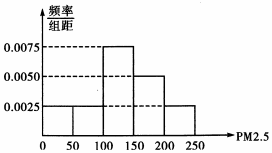 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
用频率估计概率.
(1)估计该市在下一年的360天中空气质量为一级天气的天数;
(2)在样本中,按照分层抽样的方法抽取8天的PM2.5值的数据,再从这8个数据中随机抽取5个,求一级、二级、三级、四级天气都有的概率;
(3)如果该市对环境进行治理,治理后经统计,每天PM2.5值X近似满足X~N(115,752),则治理后的PM2.5值的均值比治理前大约下降了多少?
 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级| PM2.5 | [0,100) | [100,150) | [150,200) | [200,250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
(1)估计该市在下一年的360天中空气质量为一级天气的天数;
(2)在样本中,按照分层抽样的方法抽取8天的PM2.5值的数据,再从这8个数据中随机抽取5个,求一级、二级、三级、四级天气都有的概率;
(3)如果该市对环境进行治理,治理后经统计,每天PM2.5值X近似满足X~N(115,752),则治理后的PM2.5值的均值比治理前大约下降了多少?
16.函数f(x)=|sinx+2cosx|+|2sinx-cosx|的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
13.我国从2016年1月1日起统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后和80后作为调查对象,随机调查了100位,得到数据如表:
(1)以这100个人的样本数据估计该市的总体数据,且视频率为概率,若从该市70后公民中随机抽取3位,记其中生二胎的人数为X,求随机变量X的分布列,数学期望和方差;
(2)根据调查数据,是否有90%的把握认为“生二胎与年龄有关”,并说明理由.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,是否有90%的把握认为“生二胎与年龄有关”,并说明理由.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
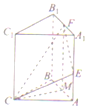 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上