题目内容
定义运算a※b为a※b=
如1※2=1,则函数f(x)=sinx※cosx的值域为 .
如1※2=1,则函数f(x)=sinx※cosx的值域为 .[-1,
]
]f(x)=sinx※cosx=
由y=sinx与y=cosx的图象知f(x)在
一个周期内的图象如图实线部分所示.
由图象可知函数值域为[-1,].
由y=sinx与y=cosx的图象知f(x)在
一个周期内的图象如图实线部分所示.由图象可知函数值域为[-1,
].
练习册系列答案
相关题目
的导函数的图像如图所示，给出下列判断：
内单调递增；
内单调递减；
内单调递增；
时，函数
时，函数
的展开中，
的幂指数是整数的项共有
，x∈R)的部分图象如图所示，则函数表达式为( )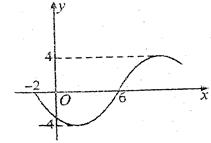
)
)
π
π
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,
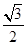),求f(θ)的值;
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
-
)(0≤x≤9)的最大值与最小值之和为( )
sinωxsin
(ω＞0)的最小正周期为
.
上的取值范围．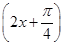
和函数y＝cos
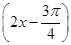的图象关于原点对称；命题q：当x＝kπ＋
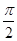(k∈Z)时，函数y＝
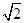(sin 2x＋cos 2x)取得极小值．下列说法正确的是( )