题目内容
8.设常数a≠0,函数$f(x)=lg\frac{x+1-2a}{x+1+3a}$.(1)当a=1时,判断并证明函数y=f(x)在(1,+∞)上的单调性.
(2)是否存在实数a,使函数y=f(x)为奇函数或偶函数?若存在,求出a的值,并判断相应的y=f(x)的奇偶性;若不存在,说明理由.
分析 (1)当a=1时,f(x)=lg$\frac{x-1}{x+4}$,利用导数法即可得出结论;
(2)假设存在,利用奇函数的定义,即可得出结论.
解答 解:(1)当a=1时,f(x)=lg$\frac{x-1}{x+4}$,
令y=$\frac{x-1}{x+4}$,则y′=$\frac{5}{(x+4)^{2}}$>0,即函数y=$\frac{x-1}{x+4}$,在(1,+∞)上单调递增,
∴函数y=f(x)在(1,+∞)上单调递增;
(2)f(-x)=lg$\frac{-x+1-2a}{-x+1+3a}$,f(-x)+f(x)=0,
可得(x-1+2a)(x+1-2a)=(x-1-3a)(x+1+3a),
∴a=-2,函数是奇函数.
点评 本题考查函数的奇偶性,考查增函数的判断,考查导数法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
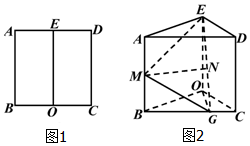 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.