题目内容
8.若对任意的x>1,函数x+xlnx≥k(3x-e)(其中e是自然对数的底数,e=2.71828…),则实数k的最大值为1.分析 根据题意,把不等式x+xlnx≥k(3x-e)化为$\frac{x+xlnx}{3x-e}$≥k,
设f(x)=$\frac{x+xlnx}{3x-e}$,x>1,利用导数求出f(x)在x∈(1,+∞)上的最小值即可.
解答 解:∵x>1,∴3x>3,∴3x-e>0;
不等式x+xlnx≥k(3x-e)可化为$\frac{x+xlnx}{3x-e}$≥k,
设f(x)=$\frac{x+xlnx}{3x-e}$,x>1;
则f′(x)=$\frac{(2+lnx)(3x-e)-3(x+xlnx)}{{(3x-e)}^{2}}$=$\frac{3x-2e-elnx}{{(3x-e)}^{2}}$,
令g(x)=3x-2e-elnx,x>1;
则g′(x)=3-$\frac{e}{x}$=$\frac{3x-e}{x}$,
令g′(x)=0,解得x=$\frac{e}{3}$<1,
∴在x∈(1,+∞)上,g′(x)>0,g(x)是单调增函数;
又g(e)=0,∴x∈(1,e)时,g(x)<0,则f′(x)<0,f(x)是单调减函数;
x∈(e,+∞)时,g(x)>0,则f′(x)>0,f(x)是单调增函数;
∴f(x)在x∈(1,+∞)上的最小值是f(x)min=f(e)=$\frac{e+elne}{3e-e}$=1;
∴1≥k,即实数k的最大值为1.
故答案为:1.
点评 本题考查了不等式的解法与应用问题,也考查了利用导数求函数的最值问题,是综合性题目.

练习册系列答案
相关题目
20.掷两枚硬币,至少有一枚出现正面朝上的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
16.若函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2ax-1,x≥1}\\{ax-1,x<1}\end{array}\right.$在R上是增函数,则实数a的取值范围是( )
| A. | 0$<a≤\frac{1}{3}$ | B. | 0<a≤1 | C. | a≤1 | D. | a>0 |
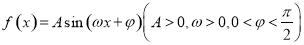 的图象经过三点
的图象经过三点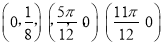 ,且在区间
,且在区间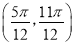 内有唯一的最值,且为最小值.
内有唯一的最值,且为最小值.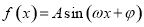 的解析式;
的解析式;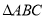 中,
中,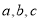 分别是角
分别是角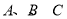 的对边,若
的对边,若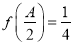 且
且 ,求
,求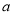 的值.
的值. ,
, ,且
,且 与
与 夹角为
夹角为 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.