题目内容
2.已知直线l1:ax-y-1=0:,l2:(a+2)x-ay+2=0(a>0),直线l1∥l2.(1)求实数a的值;
(2)是否存在一点P,它同时满足下列三个条件:①是第一象限的点:②在直线y=x上:③到直线l1的距离是它到直线l2距离的2倍.若存在.求出点P的坐标:若不存在.说明理由.
分析 (1)由题意利用两条直线平行的条件,求得a的值.
(2)由题意利用点到直线的距离公式求得m的值,从而得出结论.
解答 解:(1)由直线l1:ax-y-1=0:,l2:(a+2)x-ay+2=0(a>0),直线l1∥l2,
可得$\frac{a+2}{a}$=$\frac{-a}{-1}$≠$\frac{2}{-1}$,求得a=2,或a=-1 (舍去).
当a=2 时,直线l1:2x-y-1=0:,l2:2x-y+1=0,满足直线l1∥l2.
故a=2.
(2)设点P(m,m),m>0,由$\frac{|2m-m-1|}{\sqrt{5}}$=2•$\frac{|2m-m+1|}{\sqrt{5}}$,
可得|m-1|=2|m+1|,m2-2m+1=4(m2+2m+1),求得m=-$\frac{1}{3}$,或m=-3,
都不满足m>0,故点P不存在.
点评 本题主要考查两条直线平行的条件,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值为( )
| A. | 5 | B. | 8 | C. | $\frac{13}{2}$ | D. | 7 |
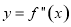 是
是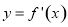 的导数.某同学经过探究发现,任意一个三次函数
的导数.某同学经过探究发现,任意一个三次函数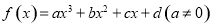 都有对称中心
都有对称中心 ,其中
,其中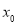 满足
满足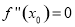 .已知函数
.已知函数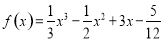 ,则
,则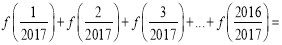 ( )
( )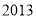 B.
B.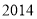 C.
C.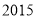 D.
D.