题目内容

7．已知数列{an}是公比为2的等比数列，且a2、a3+1、a4成等差数列，求数列{an}的前n项和Sn．

分析 由题意可得2（a3+1）=a2+a4，由公比为2，把a3、a4用a2表示，求得a2，进一步求出a1，代入等比数列的前n项和得答案．

解答 解：由题意可得2（a3+1）=a2+a4，
即2（2a2+1）=a2+4a2，解得：a2=2．
∴${a}_{1}=\frac{{a}_{2}}{2}=1$．
∴数列{an}的前n项和Sn=$\frac{1×（1-{2}^{n}）}{1-2}={2}^{n}-1$．

点评 本题考查等差数列和等比数列的通项公式，考查了等比数列的前n项和，是基础的计算题．

练习册系列答案
相关题目
17．设函数fn（x）=2anx3-3an+1x2+6x+1，an＞0，a1=1，若fn（x）有两个极值点αn，βn，且满足αn+βn-1=2nαnβn，其中n=1，2，3，…
（1）试用an表示an+1．
（2）求数列{αn}的通项公式．
（3）设Tn=$\frac{{α}_{1}+{β}_{1}-1}{{a}_{2}}$+$\frac{{α}_{2}+{β}_{2}-1}{{a}_{3}}$+…+$\frac{{α}_{n}+{β}_{n}-1}{{a}_{n+1}}$，若不等式Tn-$\frac{{n}^{2}-6n+7}{{a}_{n+1}}$$＜\frac{1}{m}$+1对一切n∈N*恒成立，求正整数m的最大值．
18．若椭圆E1：$\frac{{x}^{2}}{{a}_{1}^{2}}$+$\frac{{y}^{2}}{{b}_{1}^{2}}$=1和椭圆E2：$\frac{{x}^{2}}{{a}_{2}^{2}}$+$\frac{{y}^{2}}{{b}_{2}^{2}}$=1的离心率相同，我们称椭圆E1和E2为“同率”椭圆．
（Ⅰ）求过（1，$\frac{\sqrt{6}}{2}$）且与椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{8}$=1“同率”的椭圆C的方程；
（Ⅱ）设直线l是圆O：x2+y2=$\frac{4}{3}$上动点P（x0，y0）（x0•y0≠0）处的切线，l与椭圆C交于不同的两点Q，R，证明：∠QOR=$\frac{π}{2}$．
15．（1）已知直线l的纵截距为-1，倾斜角是直线l1：3x+4y-1=0的倾斜角的一半，求直线l的方程．
（2）已知直线l过点A（-2，4），分别交x轴、y轴于点B、C且满足$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{AC}$，求直线l的方程．
2．已知直线l1：ax-y-1=0：，l2：（a+2）x-ay+2=0（a＞0），直线l1∥l2．
（1）求实数a的值；
（2）是否存在一点P，它同时满足下列三个条件：①是第一象限的点：②在直线y=x上：③到直线l1的距离是它到直线l2距离的2倍．若存在．求出点P的坐标：若不存在．说明理由．
12．已知过原点的直线交椭圆$\frac{{x}^{2}}{3}$+y2=1于A，B两点，若点M为抛物线y=x2+2上的一个动点，则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最小值为（　　）
A．1B．2C．2-$\sqrt{3}$D．-5
19．已知一块四边形园地ABCD中，∠A=45°，∠B=60°，∠C=105°，若AB=2m，BC=1m，则该四边形园地ABCD的面积等于$\frac{3}{2}$-$\frac{\sqrt{3}}{4}$m2．
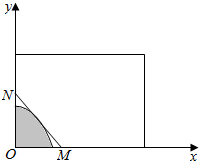16．如图，某房地产公司要在一块矩形宽阔地面上开发物业，阴影部分是不能开发的古建筑群，且要求用在一条直线上的栏栅进行隔离，古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分，栏栅与矩形区域边界交于点M、N，则当能开发的面积达到最大时，OM的长为1．

若是定义在上的偶函数，，有，则（ ）

A．

B．

C．

D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网