Question

【题目】如图所示，在多面体中，四边形与四边形均为边长为2的正方形，为等腰直角三角形，，且平面平面，平面平面．

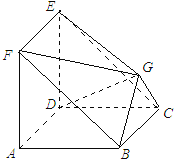
（1）求证：平面平面；

（2）求多面体的体积．

Answer 1

【答案】见解析

【解析】（1）∵平面平面，且，∴平面．……………1分

∵平面，∴．……………2分

又∵为等腰直角三角形，，∴．

∵，∴平面．……………4分

又平面，∴平面平面．……………5分

（2）取的中点，连接，，则

．……………6分

∵平面平面，，∴平面，

∴为四棱锥的高，且．……………7分

又∵平面，∴，∴平面，平面，

∴点到平面的距离就是点到平面的距离，即为2，

点到平面的距离就是点到平面的距离，即为1．……………9分

同理，点到平面的距离就是点到平面的距离，即为1，……………10分

∴

．……………12分

（或计算）

【命题意图】本题主要考查空间平面与平面的垂直关系、四棱锥的体积，意在考查逻辑思维能力、空间想

象能力、逻辑推理论证能力、计算能力．