题目内容
6.在平行四边形ABCD中,F是CD边的中点,AF与BD相交于E,则$\overrightarrow{AE}$=( )| A. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ | C. | $\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AD}$ | D. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AD}$ |
分析 根据平面向量基本定理以及三角形法则或者平行四边形法则,将所求用$\overrightarrow{AB}$,$\overrightarrow{AD}$表示.
解答  解:由题意,如图F是CD边的中点,所以DE=$\frac{1}{3}DB$,
解:由题意,如图F是CD边的中点,所以DE=$\frac{1}{3}DB$,
所以$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{1}{3}\overrightarrow{DB}$=$\overrightarrow{AD}+\frac{1}{3}(\overrightarrow{AB}-\overrightarrow{AD})$=$\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$;
故选A.
点评 本题考查了平面向量基本定理的运用以及平面向量的加法的几何意义;属于中档题.

练习册系列答案
相关题目
17.设m,n∈R,若直线mx+ny=2与圆x2+y2=1相切,则m+n的取值范围是( )
| A. | [-2,2] | B. | [-∞,-2]∪[2,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
17.函数f(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后得到的函数是奇函数,则函数f(x)的图象( )
| A. | 关于点(-$\frac{π}{3}$,0)对称 | B. | 关于直线x=-$\frac{π}{6}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
1.在6件产品中有4件合格品,2件次品,产品检验时,从中抽取3件,至少有1件次品的抽法有( )
| A. | 10 | B. | 16 | C. | 32 | D. | 24 |
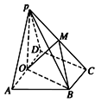 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. ,
, 满足条件
满足条件 则
则 的最大值是( )
的最大值是( )