题目内容
17.设m,n∈R,若直线mx+ny=2与圆x2+y2=1相切,则m+n的取值范围是( )| A. | [-2,2] | B. | [-∞,-2]∪[2,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
分析 由直线mx+ny=2与圆x2+y2=1相切,得m2+n2=4,从而mn≤$\frac{{m}^{2}+{n}^{2}}{2}$=2,进而(m+n)2=m2+n2+2mn≤4+2×2=8,由此能求出m+n的取值范围.
解答 解:∵m,n∈R,直线mx+ny=2与圆x2+y2=1相切,
∴圆心(0,0)到直线的距离d=$\frac{|0+0-2|}{\sqrt{{m}^{2}+{n}^{2}}}$=1,
解得m2+n2=4,
∴mn≤$\frac{{m}^{2}+{n}^{2}}{2}$=2,
∴(m+n)2=m2+n2+2mn≤4+2×2=8,
∴-2$\sqrt{2}≤m+n≤2\sqrt{2}$.
∴m+n的取值范围是[-2$\sqrt{2}$,2$\sqrt{2}$].
故选:C.
点评 本题考查代数和取值范围的求法,考查直线方程、圆、点到直线的距离公式、基本不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
8. 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
5.已知A,B是锐角三角形ABC的两个内角,设m=tanA•tanB,f(x)=logmx,则下列各式一点成立的是( )
| A. | f(cosA)>f(sinB) | B. | f(sinA)>f(cosB) | C. | f(cosA)≥f(sinB) | D. | f(sinA)≥f(cosB) |
6.在平行四边形ABCD中,F是CD边的中点,AF与BD相交于E,则$\overrightarrow{AE}$=( )
| A. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ | C. | $\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AD}$ | D. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AD}$ |
 中,
中, 底面
底面 ,底面
,底面
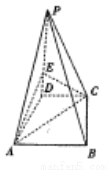
 上确定一点
上确定一点 ,使得
,使得 平面
平面 ,并求
,并求 的值;
的值; 与平面
与平面 ,则复数
,则复数 在复平面上对应的点位于( )
在复平面上对应的点位于( ) 如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.
如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1. 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.