题目内容
已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A＞0，ω＞0，0＜φ＜
)的周期为π，且图象上一个最低点为M
.
(1) 求f(x)的解析式；
(2) 当x∈
时，求f(x)的最值．
解：(1) 由最低点为M
，得A＝2.
由T＝π，得ω＝
＝2.
由点M在图象上得2sin
＝－2，
即sin＝－1，∴ 
＋φ＝2kπ－
(k∈Z)，
即φ＝2kπ－
，k∈Z.又φ∈
，
∴ φ＝
，∴ f(x)＝2sin
.
(2) ∵ x∈
，∴ 2x＋∈
.
∴ 当2x＋＝，即x＝0时，f(x)取得最小值1；
当2x＋＝
，即x＝
时，f(x)取得最大值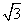
.
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
cos4x＋sin4x的最小正周期为________．
＝________．
＋cos
，x∈R.
，cos(β＋α)＝－
，求证：[f(β)]2－2＝0.
(x∈R)的图象，只需把函数y＝2sinx(x∈R)的图象上所有的点经过怎样的变换得到？
，则这个函数的解析式为________．
＝__________．
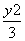＝1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则
的最小值为________．