题目内容
数列 各项均为正数,其前
各项均为正数,其前 项和为
项和为 ,且满足
,且满足 .
.
(Ⅰ)求证数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)设 , 求数列
, 求数列 的前n项和
的前n项和 ,并求使
,并求使 对所有的
对所有的 都成立的最大正整数m的值.
都成立的最大正整数m的值.
解:(Ⅰ)∵ ,∴当n≥2时,
,∴当n≥2时, ,
,
整理得, (n≥2),(2分)又
(n≥2),(2分)又 , (3分)
, (3分)
∴数列 为首项和公差都是1的等差数列. (4分)
为首项和公差都是1的等差数列. (4分)
∴ ,又
,又 ,∴
,∴ (5分)
(5分)
∴n≥2时, ,又
,又 适合此式
适合此式
∴数列 的通项公式为
的通项公式为 (7分
(7分
(Ⅱ)∵ (8分)
(8分)
∴
 =
= (10分)
(10分)
∴ ,依题意有
,依题意有 ,解得
,解得 ,
,
故所求最大正整数 的值为3 (12分)
的值为3 (12分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 +2)=x+2
+2)=x+2 等于( )
等于( ) B.
B. C.16或9 D.12
C.16或9 D.12  是坐标原点,点
是坐标原点,点 .若点
.若点 为平面区域
为平面区域 上的一个动点,则
上的一个动点,则 的取值范围是__________.
的取值范围是__________.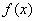 =log2(3x-1)的定义域为( )
=log2(3x-1)的定义域为( )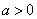 时,函数
时,函数 的图象大致是( )
的图象大致是( )
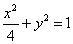 的左、右焦点.
的左、右焦点.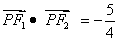 ,求点P的作标;
,求点P的作标;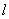 的斜率
的斜率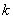 的取值范围.
的取值范围.