题目内容
已知曲线C1:
(θ为参数),C2:
(t为参数).
(Ⅰ)将C1、C2的方程化为普通方程;
(Ⅱ)若C2与C1交于M、N,与x轴交于P,求|PM|•|PN|的最小值及相应α的值.
|
|
(Ⅰ)将C1、C2的方程化为普通方程;
(Ⅱ)若C2与C1交于M、N,与x轴交于P,求|PM|•|PN|的最小值及相应α的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(I)),利用sin2θ+cos2θ=1,即可把曲线C1:
(θ为参数),化为普通方程;由C2:
(t为参数),消去参数t即可得出.
(II)C2与x轴交于P(
,0),把C2的方程代入曲线C1可得:(2+22sin2α)t2+2
tcosα-1=0.利用参数的几何意义可得|PM|•|PN|=-t1t2=
,进而求出最小值.
|
|
(II)C2与x轴交于P(
| ||
| 2 |
| 2 |
1-2
| ||
| 2+22sin2α |
解答:
解:(Ⅰ)由曲线C1:
(θ为参数),利用sin2θ+cos2θ=(
)2+x2=1,化为x2+12y2=1.
由C2:
(t为参数),消去参数t可得:(x-
)sinα-ycosα=0.
(Ⅱ)C2与x轴交于P(
,0),
把C2:
(t为参数).代入曲线C1可得:(2+22sin2α)t2+2
tcosα-1=0.
∴|PM|•|PN|=-t1t2=
≥
,
∴|PM|•|PN|的最小值
,此时α=kπ+
,k∈Z.
|
| 6y | ||
|
由C2:
|
| ||
| 2 |
(Ⅱ)C2与x轴交于P(
| ||
| 2 |
把C2:
|
| 2 |
∴|PM|•|PN|=-t1t2=
1-2
| ||
| 2+22sin2α |
| 1 |
| 24 |
∴|PM|•|PN|的最小值
| 1 |
| 24 |
| π |
| 2 |
点评:本题考查了把参数方程化为普通方程、直线参数的几何意义,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
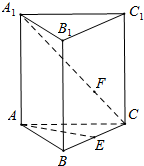 如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.
如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.