题目内容
△ABC中，A=
，AB=3，AC=8，则BC= ．
| π |
| 3 |
考点：余弦定理
专题：解三角形
分析：△ABC中，由余弦定理可得，BC2=AB2+AC2-2AB•ACcosA可求BC．
解答：
解：由余弦定理可得，BC2=AB2+AC2-2AB•ACcosA
=9+64+9-2×3×8cos60°=49，
∴BC=7，
故答案为：7．
=9+64+9-2×3×8cos60°=49，
∴BC=7，
故答案为：7．
点评：本题主要考查了利用余弦定理解三角形，属于公式的基本应用，是基础题目．
练习册系列答案
相关题目
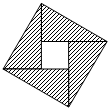三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（ ）”的几何解释．| A、如果a＞b，b＞c，那么a＞c |
| B、如果a＞b＞0，那么a2＞b2 |
| C、对任意实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立 |
| D、如果a＞b，c＞0那么ac＞bc |
已知集合A={x∈N|x＜6}，则下列关系式错误的是（ ）
| A、0∈A | B、1.5∉A |
| C、-1∉A | D、6∈A |
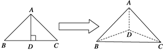如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（ ）| A、BD⊥AC | ||
| B、△ABC是等边三角形 | ||
| C、平面ADC⊥平面ABC | ||
D、二面角A-BC-D的正切值为
|
如图，三棱柱的侧棱长为2，底面是边长为2的正三角形，AA1⊥面A1B1C1，正视图是边长为2正方形．函数f（x）当x趋近于x0时极限存在是f（x）在点x0的某个去心领域内有界的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、即不充分也不必要条件 |
如图，空间四边形ABCD中，各边及对角线长均为2，E是AB的中点，过CE且平行于AD的平面交BD于F，则△CEF的面积为