题目内容
 如图所示,一个四棱锥的主视图和侧视图均为直角三角形,俯视图为矩形,则该四棱锥的四个侧面中,直角三角形的个数是( )
如图所示,一个四棱锥的主视图和侧视图均为直角三角形,俯视图为矩形,则该四棱锥的四个侧面中,直角三角形的个数是( )| A、1 | B、2 | C、3 | D、4 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:画出满足条件的四棱锥的直观图,可令棱锥PA⊥矩形ABCD,进而可得可得△PAB 和△PAD都是直角三角形,再由由线面垂直的判定定理可得CB⊥平面PAB,CD⊥平面PAD,又得到了两个直角三角形△PCB 和△PCD,由此可得直角三角形的个数.
解答:
解:满足条件的四棱锥的底面为矩形,且一条侧棱与底面垂直,
画出满足条件的直观图如图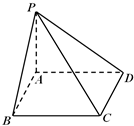 四棱锥P-ABCD所示,
四棱锥P-ABCD所示,
不妨令PA⊥矩形ABCD,
∴PA⊥AB,PA⊥AD,PA⊥CB,PA⊥CD,
故△PAB 和△PAD都是直角三角形.
又矩形中 CB⊥AB,CD⊥AD.
这样CB垂直于平面PAB内的两条相交直线PA、AB,
CD垂直于平面PAD内的两条相交直线 PA、AD,
由线面垂直的判定定理可得CB⊥平面PAB,CD⊥平面PAD,
∴CB⊥PB,CD⊥PD,故△PCB 和△PCD都是直角三角形.
故直角三角形有△PAB、△PAD、△PBC、△PCD共4个.
故选D.
画出满足条件的直观图如图
 四棱锥P-ABCD所示,
四棱锥P-ABCD所示,不妨令PA⊥矩形ABCD,
∴PA⊥AB,PA⊥AD,PA⊥CB,PA⊥CD,
故△PAB 和△PAD都是直角三角形.
又矩形中 CB⊥AB,CD⊥AD.
这样CB垂直于平面PAB内的两条相交直线PA、AB,
CD垂直于平面PAD内的两条相交直线 PA、AD,
由线面垂直的判定定理可得CB⊥平面PAB,CD⊥平面PAD,
∴CB⊥PB,CD⊥PD,故△PCB 和△PCD都是直角三角形.
故直角三角形有△PAB、△PAD、△PBC、△PCD共4个.
故选D.
点评:本题主要考查证明线线垂直、线面垂直的方法,以及棱锥的结构特征,属于基础题.

练习册系列答案
相关题目
设x∈R,向量
=(2,x),
=(3,-2),且
⊥
,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | ||
B、
| ||
C、2
| ||
| D、6 |
某市对10000名中学生的数学成绩(满分100分)进行抽样统计,发现他们近似服从正态分布N~(70,102),若90分以上者有230人,则这10000名学生中分数在50分到90分之间的人数约有( )
| A、7140人 | B、230人 |
| C、9540人 | D、4770人 |
直线y-x+1=0和圆x2+y2-4y=0的位置关系为( )
| A、相交 | B、相切 |
| C、相离 | D、无法判断 |
经过点A(1,0),B(0,1)的直线方程为( )
| A、y=x+1 |
| B、y=x-1 |
| C、y=-x+1 |
| D、y=-x-1 |
 根据两个变量x,y之间的观测数据画成散点图如图所示,这两个变量是否具有线性相关关系
根据两个变量x,y之间的观测数据画成散点图如图所示,这两个变量是否具有线性相关关系