题目内容
函数y=log2(x2-3x+2)的递减区间是( )
| A、(-∞,1) | ||
| B、(2,+∞) | ||
C、(-∞,
| ||
D、(
|
考点:复合函数的单调性
专题:函数的性质及应用
分析:设t=x2-3x+2,根据复合函数单调性之间的关系进行求解即可.
解答:
解:由x2-3x+2>0,得x<1或x>2,
设t=x2-3x+2,则y═log2t为增函数,
则根据复合函数单调性之间的关系知要求函数y=log2(x2-3x+2)的递减区间,
即求函数t=x2-3x+2的递减区间,
∵t=x2-3x+2的递减区间为(-∞,1),
∴函数y=log2(x2-3x+2)的递减区间是(-∞,1),
故选:A.
设t=x2-3x+2,则y═log2t为增函数,
则根据复合函数单调性之间的关系知要求函数y=log2(x2-3x+2)的递减区间,
即求函数t=x2-3x+2的递减区间,
∵t=x2-3x+2的递减区间为(-∞,1),
∴函数y=log2(x2-3x+2)的递减区间是(-∞,1),
故选:A.
点评:本题主要考查函数单调性的求解,根据复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设a=20.1,b=ln2,c=log3
,则( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
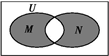 已知全集U=R,集合M={x|y=
已知全集U=R,集合M={x|y=| 3-x2 |
| π |
| 4 |
A、[-3,-
| ||||
B、(1,
| ||||
C、[-3,-
| ||||
D、[-3,-
|
sin(-
)的值等于( )
| 21π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
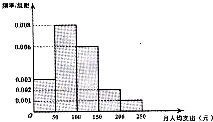 如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )
如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )