题目内容
12.在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.(1)求角A的值;
(2)若$b+c=\sqrt{10}\;,\;\;a=2$,求△ABC的面积S.
分析 (1)由已知利用正弦定理,三角函数恒等变换的应用化简可得sinB=2sinBcosA,结合sinB≠0,可求cosA,进而可求A的值.
(2)由已知及余弦定理,平方和公式可求bc的值,进而利用三角形面积公式即可计算得解.
解答 解:(1)在△ABC中,∵acosC+ccosA=2bcosA,
∴sinAcosC+sinCcosA=2sinBcosA,
∴sin(A+C)=sinB=2sinBcosA,
∵sinB≠0,
∴$cosA=\frac{1}{2}$,可得:$A=\frac{π}{3}$.
(2)∵$cosA=\frac{1}{2}=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$,$b+c=\sqrt{10}\;,\;\;a=2$,
∴b2+c2=bc+4,可得:(b+c)2=3bc+4=10,可得:bc=2.
∴$S=\frac{1}{2}bcsinA=\frac{{\sqrt{3}}}{2}$.
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,余弦定理,平方和公式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.在等差数列{an}中,a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,类比上述性质,相应地在等比数列{bn}中,若b9=1,则成立的等式是( )
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
7.等差数列{an}的前n项和为Sn,且S3=6,S6=3,则S10=( )
| A. | $\frac{1}{10}$ | B. | 0 | C. | -10 | D. | -15 |
4. “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
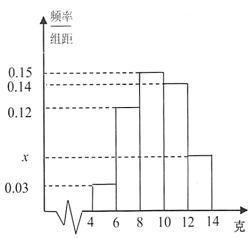
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
 “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:| 累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
| 等级 | P1 | P2 | P3 | P4 |
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
16.定义在R上的奇函数f(x)关于点(2,1)对称,则f(6)=( )
| A. | 9 | B. | 7 | C. | 5 | D. | 3 |
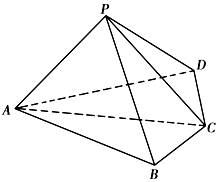 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.