题目内容
(本 小题满分12分)在直三棱柱
小题满分12分)在直三棱柱 ABC—A1B1C1中,CA=CB=CC1=2,
ABC—A1B1C1中,CA=CB=CC1=2, ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.
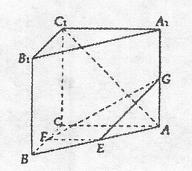
 小题满分12分)在直三棱柱
小题满分12分)在直三棱柱 ABC—A1B1C1中,CA=CB=CC1=2,
ABC—A1B1C1中,CA=CB=CC1=2, ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.

(Ⅰ)G即是AA1的中点
(Ⅱ)AC1与平面EFG所成角
(Ⅱ)AC1与平面EFG所成角

(Ⅰ)以C为原点,分别以CB、CA、CC1
为x轴、y轴、z轴建立空间直角坐标系,
则F(1,0,0),E(1,1,0),A(0,2,0),
C1(0,0,2), …………2分
…………2分
设G(0,2,h),则
 …………4分
…………4分


 即是AA1的中点 …………6分
即是AA1的中点 …………6分
(Ⅱ)设 是平面EFG的法向量,
是平面EFG的法向量,
则 。
。
所以 平面EFG的一个法向量
平面EFG的一个法向量 …………8分
…………8分
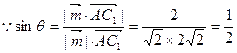 …………10分
…………10分
 即AC1与平面EFG所成角
即AC1与平面EFG所成角 …………12分
…………12分
为x轴、y轴、z轴建立空间直角坐标系,
则F(1,0,0),E(1,1,0),A(0,2,0),
C1(0,0,2),
 …………2分
…………2分设G(0,2,h),则

 …………4分
…………4分

 即是AA1的中点 …………6分
即是AA1的中点 …………6分(Ⅱ)设
 是平面EFG的法向量,
是平面EFG的法向量,则
 。
。所以
 平面EFG的一个法向量
平面EFG的一个法向量 …………8分
…………8分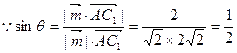 …………10分
…………10分 即AC1与平面EFG所成角
即AC1与平面EFG所成角 …………12分
…………12分
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
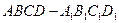 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系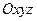 ,
,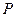 在线段
在线段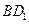 上,且满足
上,且满足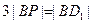 ,试写出点
,试写出点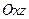 的对称点
的对称点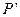 的坐标;
的坐标;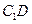 中点为
中点为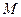 ,求点
,求点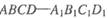 中,直线
中,直线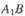 与平面
与平面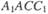 所成的角为
所成的角为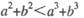 (B)
(B)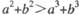
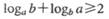 (D)
(D)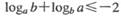





 内的一条直线,P为
内的一条直线,P为 ,则必有( )
,则必有( )
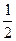


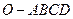 中,
中,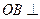 底面
底面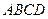 ,且
,且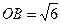 ,底面
,底面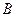 在平面
在平面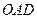 内的射影
内的射影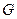 恰为
恰为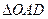 的重心.
的重心.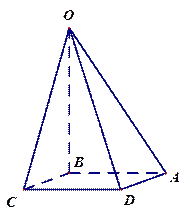 ①求
①求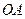 的长;
的长;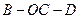 的平面角的余弦值.
的平面角的余弦值. 中,
中, ,
, ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )

