题目内容
已知以F为焦点的抛物线y2=4x上的两点A、B满足
=3
，则弦AB的中点到准线的距离为（ ）
A．
B．
C．2 D．1
A
【解析】
试题分析：抛物线的焦点为
，准线方程为
设
，直线AB的方程为：
由
消法
得：
（*）
由题设知：
是方程的两根，所以
（1）
又因为
=3
，所以
（2）
解由方程（1）（2）组成的方程组得：
所以
设弦AB的中点为C
，则
，所以C到准线的距离
故选A.
考点：1、抛物线的标准方程与几何性质；2、直线与抛物线的位置关系．
练习册系列答案
快乐5加2金卷系列答案
相关题目
B．
D．
，
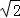），半径r=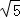
的概率为 _________ ．
的最小值；
都有
，求实数
的取值范围．
B．
C．
D．
为实数，且
，
为实数，且
，则A∩B的元素个数为