题目内容
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为(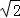 ,
, ),半径r=
),半径r=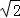 ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;(2)求|PA||PB|的值.
(1) ;(2)|PA||PB|=|PD|2=8.
;(2)|PA||PB|=|PD|2=8.
【解析】
试题分析:(1)利用 求出圆心在直角坐标系下的坐标,写出其标准方程;
求出圆心在直角坐标系下的坐标,写出其标准方程;
(2)设圆的过点C的切线与圆相切于点D,根据切割线定理,只要求出切线CD长即可.
试题解析:【解析】
(1)圆C的圆心的极坐标为C( ,
, ),
),
∴x= =1,y=
=1,y= =1,
=1,
∴圆C的直角坐标方程为(x﹣1)2+(y﹣1)2=2.
(2)点P的极坐标为(2,π),化为直角坐标P(﹣2,0).
当直线l与圆C相切于点D时,则|PD|2=|PC|2﹣r2=(﹣2﹣1)2+(0﹣1)2﹣ =8.
=8.
∴|PA||PB|=|PD|2=8.
考点:1、极坐标与参数方程;2、直线与圆的位置关系.

练习册系列答案
相关题目
 ,
, .
. 时,求函数
时,求函数 的单调区间;
的单调区间; ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 内任取一点,取到函数
内任取一点,取到函数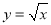 的图象与
的图象与 轴正半轴之间(阴影部分)的点的概率等于( )
轴正半轴之间(阴影部分)的点的概率等于( )
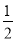 B.
B.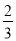
 D.
D.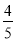
 =3
=3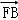 ,则弦AB的中点到准线的距离为( )
,则弦AB的中点到准线的距离为( )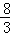 B.
B.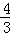 C.2 D.1
C.2 D.1 ﹣
﹣ =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x C.y=±
x C.y=± x D.y=±
x D.y=± x
x
 =3
=3 ,则弦AB的中点到准线的距离为( )
,则弦AB的中点到准线的距离为( ) B.
B. C.2 D.1
C.2 D.1 ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”; 、
、 是简单命题,若“
是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题; 是
是 的必要不充分条件;
的必要不充分条件;
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数
 的方程为
的方程为 ,则点
,则点 到直线
到直线 的距离为 .
的距离为 .