题目内容
(本小题满分14分)已知函数
(1)求函数 的最小值;
的最小值;
(2)若对所有 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.
(1)  ; (2)
; (2) 的取值范围是
的取值范围是 .
.
【解析】
试题分析:(1)由已知得 ,可得函数f (x)在
,可得函数f (x)在 上单调减函数,在
上单调减函数,在 上是单调增函数,当x=-1时,
上是单调增函数,当x=-1时, 的有极小值也是最小值,即可求出最小值;(2)令
的有极小值也是最小值,即可求出最小值;(2)令 ,则
,则 ,
,  .然后再对a进行分类讨论,根据函数单调性,解不等式即可求出结果.
.然后再对a进行分类讨论,根据函数单调性,解不等式即可求出结果.
试题解析:(1)由已知得 , 1分
, 1分
令 ;令
;令 .
.
因此,函数f (x)在 上单调减函数,在
上单调减函数,在 上是单调增函数, 5分
上是单调增函数, 5分
当x=-1时, 的有极小值也是最小值,
的有极小值也是最小值, 6分
6分
(2)令 ,
,
则 ,
,  . 8分
. 8分
(a)当 ,即
,即 时,
时, ,g(x)在
,g(x)在 是减函数,因此当
是减函数,因此当 时,都有
时,都有 ,即
,即 ; 10分
; 10分
(b)当 时,令
时,令 ;令
;令 ,
,
因此函数 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
由于对所有 都有
都有 ,即
,即 成立,
成立,
因此 ,
, ,
, ,
,
所以 . 13分
. 13分
综上所述,a的取值范围是 . 14分.
. 14分.
考点:1.应用导数研究函数的单调性、最值;2.不等式恒成立问题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 (
( ).
). 时,讨论函数
时,讨论函数 的单调性;
的单调性; 及任意
及任意 ,
, ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. ﹣
﹣ =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x C.y=±
x C.y=± x D.y=±
x D.y=± x
x =3
=3 ,则弦AB的中点到准线的距离为( )
,则弦AB的中点到准线的距离为( ) B.
B. C.2 D.1
C.2 D.1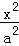 ﹣
﹣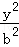 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为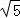 ,则C的渐近线方程为( )
,则C的渐近线方程为( )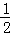 x C.y=±
x C.y=± x D.y=±
x D.y=±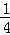 x
x ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”; 、
、 是简单命题,若“
是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题; 是
是 的必要不充分条件;
的必要不充分条件;
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数
 均为单位向量,且
均为单位向量,且 ,则
,则 与
与 夹角为( )
夹角为( )  B.
B. C.
C. D.
D.
 是定义在
是定义在 上的奇函数,则
上的奇函数,则 = .
= . ,
, ,则
,则 的最小值是 .
的最小值是 .