题目内容
已知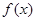 的导函数
的导函数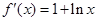 ,且
,且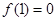 ,设
,设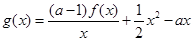 ,
,
且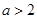 .
.
(Ⅰ)讨论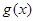 在区间
在区间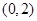 上的单调性;
上的单调性;
(Ⅱ)求证: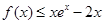 ;
;
(Ⅲ)求证: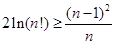 .
.
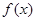 的导函数
的导函数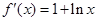 ,且
,且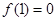 ,设
,设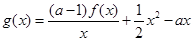 ,
,且
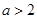 .
.(Ⅰ)讨论
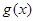 在区间
在区间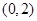 上的单调性;
上的单调性;(Ⅱ)求证:
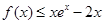 ;
;(Ⅲ)求证:
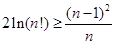 .
. 减 ,
减 , 和
和 增 ;(2)(3)详见解析
增 ;(2)(3)详见解析试题分析:(Ⅰ)利用
 的导函数找到原函数即可研究
的导函数找到原函数即可研究 的单调性, (Ⅱ)把证明不等式
的单调性, (Ⅱ)把证明不等式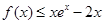 转化为证明不等式
转化为证明不等式 ,然后通过求导研究函数的值域, (Ⅲ)难点①转化
,然后通过求导研究函数的值域, (Ⅲ)难点①转化 ,②注意运用第(Ⅱ)问产生的新结论
,②注意运用第(Ⅱ)问产生的新结论 .导致
.导致 ③放缩
③放缩 后进行数列求和.
后进行数列求和.试题解析:(Ⅰ)由
 且
且 得
得 .
. 定义域为
定义域为

令
 ,得
,得 或
或 
当
 时,由
时,由 ,得
,得 ;由
;由  ,得
,得 ,或
,或
 在
在 上单调递减,在
上单调递减,在 和
和 上单调递增.
上单调递增. 当
 时, 由
时, 由 ,得
,得 ;由
;由  ,得
,得 ,
,  在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增. (Ⅱ)设
 ,令
,令 ,得
,得 ,
, ,得
,得 ,
, 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增. 在
在 处有极大值,即最大值0,
处有极大值,即最大值0,  同理可证
同理可证 ,
, 即
即
(Ⅲ)由(2)知,


又


即
 当
当 时取等号.
时取等号.
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
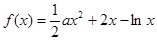
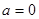 时,求
时,求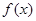 的极值;
的极值; 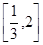 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.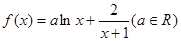 .
.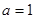 时,求
时,求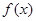 在
在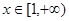 最小值;
最小值;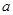 的取值范围;
的取值范围;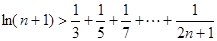 (
(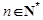 ).
).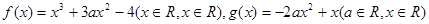 (Ⅰ)若函数
(Ⅰ)若函数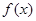 在
在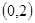 上单调递减,在区间
上单调递减,在区间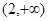 单调递增,求
单调递增,求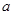 的值;
的值;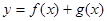 在
在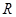 上有两个不同的极值点,求
上有两个不同的极值点,求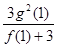 的取值范围;
的取值范围;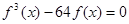 有且只有三个不同的实根,求
有且只有三个不同的实根,求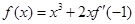 ,则函数
,则函数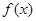 在区间
在区间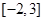 上的值域是_____________.
上的值域是_____________. 函数
函数
 图像以
图像以 为对称中心,求实数
为对称中心,求实数 和
和 的值
的值 ,求函数
,求函数 上的最小值
上的最小值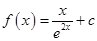 (
(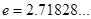 是自然对数的底数,
是自然对数的底数,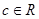 ).
).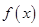 的单调区间、最大值;
的单调区间、最大值;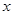 的方程
的方程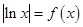 根的个数。
根的个数。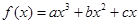 在点
在点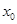 处取得极小值-4,使其导数
处取得极小值-4,使其导数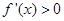 的
的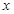 的取值范围为
的取值范围为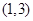 ,求:
,求: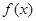 的解析式;
的解析式;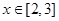 ,求
,求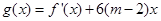 的最大值;
的最大值;