题目内容
已知函数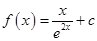 (
(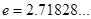 是自然对数的底数,
是自然对数的底数,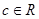 ).
).
(Ⅰ)求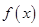 的单调区间、最大值;
的单调区间、最大值;
(Ⅱ)讨论关于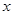 的方程
的方程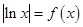 根的个数。
根的个数。
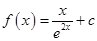 (
(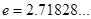 是自然对数的底数,
是自然对数的底数,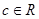 ).
).(Ⅰ)求
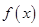 的单调区间、最大值;
的单调区间、最大值;(Ⅱ)讨论关于
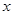 的方程
的方程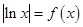 根的个数。
根的个数。解法一 (Ⅰ)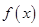 的单调递增区间为
的单调递增区间为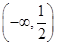 ,单调递减区间为
,单调递减区间为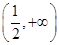 ,
,
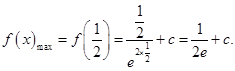
(Ⅱ)当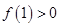 即
即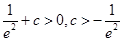 时,函数
时,函数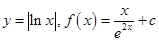 的图象有两个交点,即方程
的图象有两个交点,即方程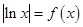 有两个根.
有两个根.
当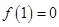 即
即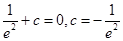 时,函数
时,函数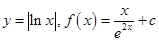 的图象有一个交点,即方程
的图象有一个交点,即方程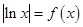 有一个根.
有一个根.
显然当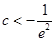 时,方程
时,方程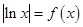 没有根.
没有根.
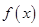 的单调递增区间为
的单调递增区间为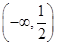 ,单调递减区间为
,单调递减区间为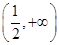 ,
,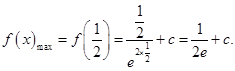
(Ⅱ)当
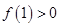 即
即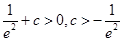 时,函数
时,函数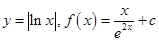 的图象有两个交点,即方程
的图象有两个交点,即方程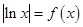 有两个根.
有两个根.当
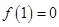 即
即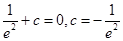 时,函数
时,函数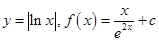 的图象有一个交点,即方程
的图象有一个交点,即方程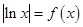 有一个根.
有一个根.显然当
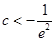 时,方程
时,方程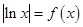 没有根.
没有根.(Ⅰ)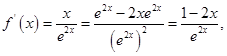
当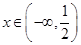 时,
时,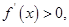 ;当
;当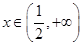 时
时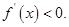
所以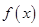 的单调递增区间为
的单调递增区间为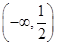 ,单调递减区间为
,单调递减区间为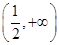 ,
,

(Ⅱ)
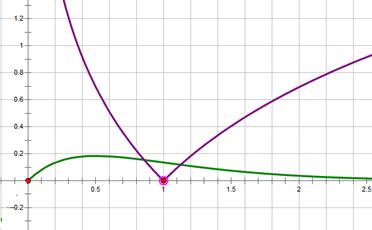
通过图象可对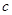 进行讨论:
进行讨论:
当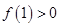 即
即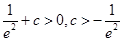 时,函数
时,函数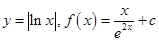 的图象有两个交点,即方程
的图象有两个交点,即方程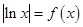 有两个根.
有两个根.
当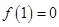 即
即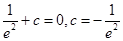 时,函数
时,函数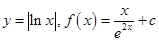 的图象有一个交点,即方程
的图象有一个交点,即方程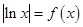 有一个根.
有一个根.
显然当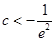 时,方程
时,方程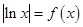 没有根.
没有根.
解法二 (Ⅰ)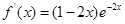 ,
,
由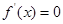 ,解得
,解得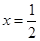 ,
,
当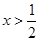 时,
时,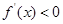 ,
,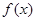 单调递减
单调递减
所以,函数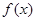 的单调递增区间是
的单调递增区间是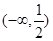 ,单调递减区间是
,单调递减区间是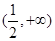 ,
,
最大值为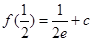
(Ⅱ)令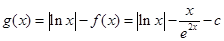
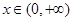
(1)当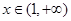 时,
时,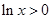 ,则
,则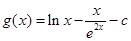 ,
,
所以,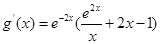
因为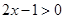 ,
,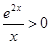 所以
所以 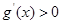
因此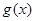 在
在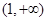 上单调递增.
上单调递增.
(2)当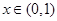 时,当时,
时,当时,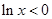 ,则
,则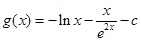 ,
,
所以,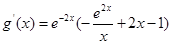
因为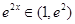 ,
,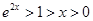 ,又
,又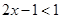
所以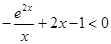 所以
所以 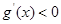
因此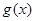 在
在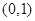 上单调递减.
上单调递减.
综合(1)(2)可知 当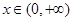 时,
时,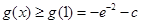 ,
,
当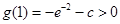 ,即
,即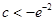 时,
时,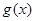 没有零点,
没有零点,
故关于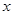 的方程
的方程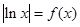 根的个数为0;
根的个数为0;
当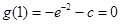 ,即
,即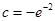 时,
时,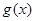 只有一个零点,
只有一个零点,
故关于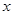 的方程
的方程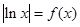 根的个数为1;
根的个数为1;
当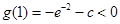 ,即
,即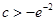 时,
时,
①当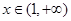 时,由(Ⅰ)知
时,由(Ⅰ)知
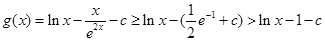
要使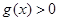 ,只需使
,只需使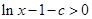 ,即
,即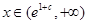 ;
;
②当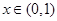 时,由(Ⅰ)知
时,由(Ⅰ)知
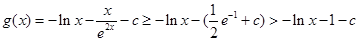 ;
;
要使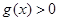 ,只需使
,只需使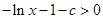 ,即
,即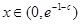 ;
;
所以当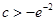 时,
时,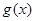 有两个零点,故关于
有两个零点,故关于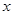 的方程
的方程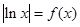 根的个数为2;
根的个数为2;
综上所述:
当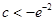 时,关于
时,关于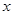 的方程
的方程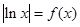 根的个数为0;
根的个数为0;
当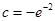 时,关于
时,关于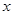 的方程
的方程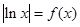 根的个数为1;
根的个数为1;
当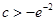 时,关于
时,关于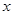 的方程
的方程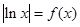 根的个数为2.
根的个数为2.
【考点定位】本题考查了函数的单调性、函数的最值等主干知识,考查了数形结合思想、分类讨论思想、函数与方程思想的综合应用.第一问的研究为第二问进行数形结合铺平了“道路”,使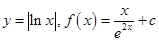 的相对位置关系更明晰.
的相对位置关系更明晰.
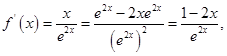
当
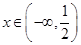 时,
时,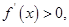 ;当
;当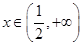 时
时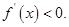
所以
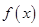 的单调递增区间为
的单调递增区间为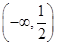 ,单调递减区间为
,单调递减区间为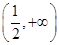 ,
,
(Ⅱ)

通过图象可对
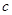 进行讨论:
进行讨论:当
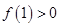 即
即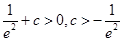 时,函数
时,函数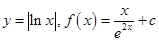 的图象有两个交点,即方程
的图象有两个交点,即方程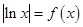 有两个根.
有两个根.当
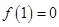 即
即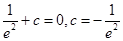 时,函数
时,函数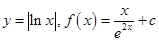 的图象有一个交点,即方程
的图象有一个交点,即方程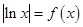 有一个根.
有一个根.显然当
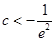 时,方程
时,方程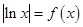 没有根.
没有根.解法二 (Ⅰ)
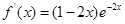 ,
,由
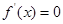 ,解得
,解得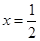 ,
,当
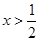 时,
时,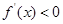 ,
,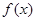 单调递减
单调递减所以,函数
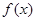 的单调递增区间是
的单调递增区间是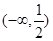 ,单调递减区间是
,单调递减区间是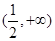 ,
,最大值为
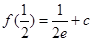
(Ⅱ)令
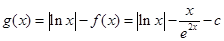
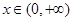
(1)当
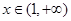 时,
时,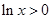 ,则
,则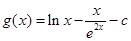 ,
,所以,
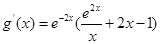
因为
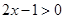 ,
,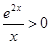 所以
所以 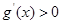
因此
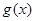 在
在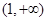 上单调递增.
上单调递增.(2)当
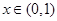 时,当时,
时,当时,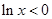 ,则
,则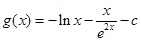 ,
,所以,
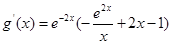
因为
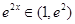 ,
,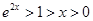 ,又
,又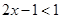
所以
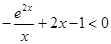 所以
所以 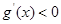
因此
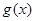 在
在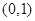 上单调递减.
上单调递减.综合(1)(2)可知 当
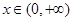 时,
时,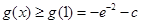 ,
,当
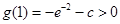 ,即
,即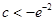 时,
时,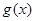 没有零点,
没有零点,故关于
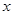 的方程
的方程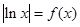 根的个数为0;
根的个数为0;当
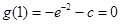 ,即
,即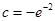 时,
时,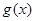 只有一个零点,
只有一个零点,故关于
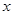 的方程
的方程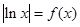 根的个数为1;
根的个数为1;当
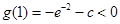 ,即
,即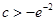 时,
时,①当
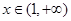 时,由(Ⅰ)知
时,由(Ⅰ)知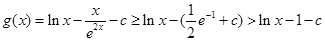
要使
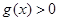 ,只需使
,只需使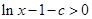 ,即
,即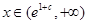 ;
;②当
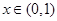 时,由(Ⅰ)知
时,由(Ⅰ)知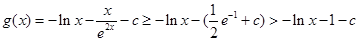 ;
;要使
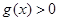 ,只需使
,只需使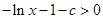 ,即
,即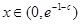 ;
;所以当
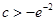 时,
时,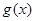 有两个零点,故关于
有两个零点,故关于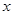 的方程
的方程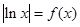 根的个数为2;
根的个数为2;综上所述:
当
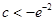 时,关于
时,关于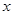 的方程
的方程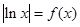 根的个数为0;
根的个数为0;当
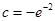 时,关于
时,关于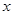 的方程
的方程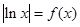 根的个数为1;
根的个数为1;当
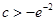 时,关于
时,关于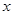 的方程
的方程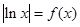 根的个数为2.
根的个数为2.【考点定位】本题考查了函数的单调性、函数的最值等主干知识,考查了数形结合思想、分类讨论思想、函数与方程思想的综合应用.第一问的研究为第二问进行数形结合铺平了“道路”,使
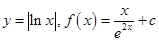 的相对位置关系更明晰.
的相对位置关系更明晰.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
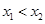 ,求证:
,求证: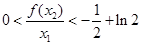 .
.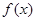 的导函数
的导函数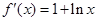 ,且
,且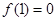 ,设
,设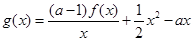 ,
,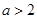 .
.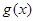 在区间
在区间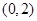 上的单调性;
上的单调性;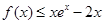 ;
;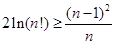 .
.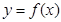 定义域为
定义域为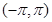 ,且函数
,且函数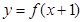 的图象关于直线
的图象关于直线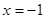 对称,当
对称,当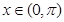 时,
时,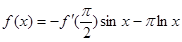 ,(其中
,(其中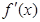 是
是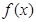 的导函数),若
的导函数),若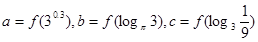 ,则
,则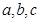 的大小关系是( )
的大小关系是( )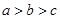
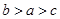
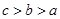
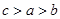
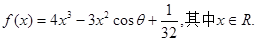
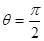 时,判断函数
时,判断函数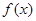 是否有极值;
是否有极值;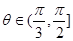 时,
时,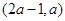 上的增函数,求实数
上的增函数,求实数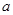 的取值范围.
的取值范围. 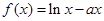 ,
,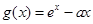 ,其中
,其中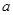 为实数.
为实数.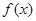 在
在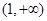 上是单调减函数,且
上是单调减函数,且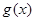 在
在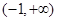 上是单调增函数,试求
上是单调增函数,试求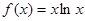 ,若
,若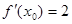 ,则
,则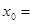 ( )
( )
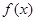 是定义在
是定义在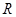 上的奇函数,
上的奇函数,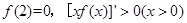 ,则不等式
,则不等式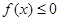 的解集是
的解集是 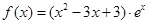 .
.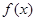 的单调区间;
的单调区间;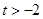 时,判断
时,判断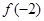 和
和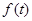 的大小,并说明理由;
的大小,并说明理由;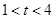 时,关于
时,关于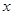 的方程:
的方程: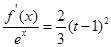 在区间
在区间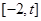 上总有两个不同的解.
上总有两个不同的解.