题目内容
从7名运动员中选出4名运动员组成接力队,参加4×100米接力赛,那么甲乙两人都不跑中间两棒的概率为 (结果用最简分数作答).
考点:古典概型及其概率计算公式
专题:概率与统计
分析:求出从7名运动员中选出4名运动员参加4×100米接力赛的不同方法有多少,再求选出的4人中甲、乙两人都不跑中间两棒的种数,求出对应的概率.
解答:
解:从7名运动员中选出4名运动员,不同的选法是
,参加4×100米接力赛的不同方式有
,
∴共有
•
=840种;
选出的4人中甲、乙两人都不跑中间两棒的不同选法是:
第一步,安排中间2个位置有
=20种,
第二步,安排首尾2个位置有
=20种,
共有20×20=400种,
∴甲乙两人都不跑中间两棒的概率为
P=
=
.
故答案为:
.
| C | 4 7 |
| A | 4 4 |
∴共有
| C | 4 7 |
| A | 4 4 |
选出的4人中甲、乙两人都不跑中间两棒的不同选法是:
第一步,安排中间2个位置有
| A | 2 5 |
第二步,安排首尾2个位置有
| A | 2 5 |
共有20×20=400种,
∴甲乙两人都不跑中间两棒的概率为
P=
| 400 |
| 840 |
| 10 |
| 21 |
故答案为:
| 10 |
| 21 |
点评:本题考查了古典概型的概率的计算问题,解题的关键是求出对应的不同选法种数是多少.

练习册系列答案
相关题目
已知圆C:x2+y2=4,若点P(x0,y0)在圆C外,则直线l:x0x+y0y=4与圆C的位置关系为( )
| A、相离 | B、相切 |
| C、相交 | D、不能确定 |
已知等差数列{an}的公差为d=3,若a1,a2,a3,a4,a5的平均数为18,则a1的值为( )
| A、12 | B、-12 |
| C、24 | D、-24 |
已知函数f(x)=ex-mx+1的图象为曲线C,若曲线C不存在与直线y=
x垂直的切线,则实数m的取值范围是( )
| 1 |
| 2 |
| A、m>2 | ||
B、m>-
| ||
| C、m≤2 | ||
D、m≤-
|
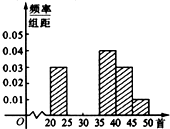 某校开展校园文化活动,其中一项是背诵古诗100首,在该项进行一段时间后,随机抽取40人,统计调查了他们会背古诗的首数,得到的数据如下:
某校开展校园文化活动,其中一项是背诵古诗100首,在该项进行一段时间后,随机抽取40人,统计调查了他们会背古诗的首数,得到的数据如下: