题目内容
如图,线段 =8,点
=8,点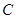 在线段
在线段 上,且
上,且 =2,
=2, 为线段
为线段 上一动点,点
上一动点,点 绕点
绕点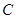 旋转后与点
旋转后与点 绕点
绕点 旋转后重合于点
旋转后重合于点 .设
.设 =
=

 的面积为
的面积为 .则
.则 的最大值为( ).
的最大值为( ).
A B. 2 C.3 D.
B. 2 C.3 D. 
A
解析试题分析:三角形的周长是一个定值8,由题意, ,故其面积可用海伦公式表示出来即
,故其面积可用海伦公式表示出来即 ,
, ,在
,在 中,
中, ,解得
,解得 ,令
,令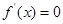 ,解得
,解得 ,∵
,∵ 上
上 ,
, ,
, ∴
∴ 的最大值为
的最大值为 ,故答案为A.
,故答案为A.
考点:导数在最大值、最小值问题中的应用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
曲线 与直线
与直线 及
及 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
若曲线 在点
在点 处切线与坐标轴围成的三角形的面积为
处切线与坐标轴围成的三角形的面积为 ,则
,则 ( )
( )
A. | B. | C. | D. |
某人进行了如下的“三段论”推理:如果 ,则
,则 是函数
是函数 的极值点,因为函数
的极值点,因为函数 在
在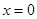 处的导数值
处的导数值 ,所以
,所以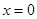 是函数
是函数 的极值点.你认为以上推理的 ( )
的极值点.你认为以上推理的 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
已知二次函数 的导数
的导数 ,且
,且 的值域为
的值域为 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B. | C.2 | D. |
已知函数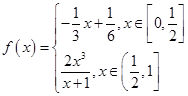 ,函数
,函数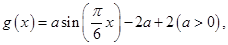 若存在
若存在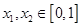 ,使得
,使得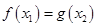 成立,则实数
成立,则实数 的取值范围( )
的取值范围( )
A.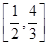 | B.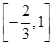 | C.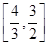 | D.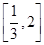 |
已知函数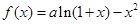 ,当
,当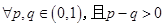 时,不等式
时,不等式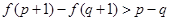 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A.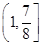 | B.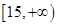 | C.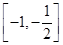 | D.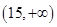 |
曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. | B. | C. | D. |
曲线 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A. | B. | C. | D. |