题目内容
5.若曲线${C_1}:y=1+\sqrt{-{x^2}+2x}$与曲线C2:(y-1)•(y-kx-2k)=0有四个不同的交点,则实数k的取值范围为($\frac{1}{2}$,$\frac{3}{4}$).分析 作出两曲线图象,根据交点个数判断直线的斜率范围即可.
解答 解:由y=1+$\sqrt{-{x}^{2}+2x}$得(x-1)2+(y-1)2=1(y≥1),
曲线C1表示以(1,1)为圆心以1为半径的上半圆,
显然直线y=1与曲线C1有两个交点,交点为半圆的两个端点.
∴直线y=kx+2k=k(x+2)与半圆有2个除端点外的交点,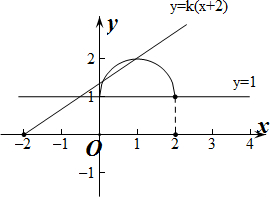
当直线y=k(x+2)经过点(0,1)时,k=$\frac{1}{2}$,
当直线y=k(x+2)与半圆相切时,$\frac{|3k-1|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{3}{4}$或k=0(舍),
∴当$\frac{1}{2}$<k<$\frac{3}{4}$时,直线y=k(x+2)与半圆有2个除端点外的交点,
故答案为:$(\frac{1}{2},\frac{3}{4})$
点评 本题考查了方程解与函数图象的关系,直线与圆的位置关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在△ABC中,若(a+b+c)(b+c-a)=3bc,则∠A等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}或\frac{2π}{3}$ |
13.命题“方程x2-4=0的解是x=±2”中,使用的逻辑联结词的情况是( )
| A. | 没有使用联结词 | B. | 使用了逻辑联结词“或” | ||
| C. | 使用了逻辑联结词“且” | D. | 使用了逻辑联结词“非” |
17.通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如右的列联表,经计算,统计量K2的观测值k2≈5.762,参照附表,则所得到的统计学结论为:有( )把握认为“爱好该项运动与性别有关”.
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| A. | 0.25% | B. | 2.5% | C. | 97.5% | D. | 99.75% |
14.设集合M={3,a},N={x|x2-3x<0,x∈Z},M∩N={1},则M∪N为( )
| A. | {1,3,a} | B. | {1,2,3,a} | C. | {1,2,3} | D. | {1,3} |