题目内容
已知各项均不相等的等差数列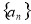 的前四项和
的前四项和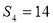 ,且
,且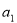 ,
,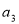 ,
,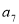 成等比数列.
成等比数列.
(Ⅰ)求数列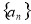 的通项公式;
的通项公式;
(Ⅱ)设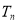 为数列
为数列 的前
的前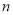 项和,若
项和,若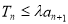 对一切
对一切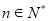 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)用待定系数法,将已知全部转化为 ,
, 的式子,设公差为
的式子,设公差为 ,由已知得
,由已知得 解得
解得 或
或 (舍去),故
(舍去),故 ;(Ⅱ)
;(Ⅱ)
 ,
, ,由
,由 对一切
对一切 恒成立,得
恒成立,得 对一切
对一切 恒成立即
恒成立即 恒成立.
恒成立.
试题解析:(Ⅰ)设公差为 ,由已知得
,由已知得 解得
解得 或
或 (舍去),
(舍去),
 ,故
,故 . 4分
. 4分
(Ⅱ) 6分
6分
 8分
8分
 ,
, ,
,  ,
, 
即 恒成立. 10分
恒成立. 10分
 ,即
,即 的最小值为
的最小值为 . 12分
. 12分
考点:数列及其应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 则z=x+2y的取值范围是( )
则z=x+2y的取值范围是( )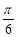 ] B.[0,
] B.[0, 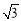 ] C.[0,
] C.[0,  在
在 上是减函数,则
上是减函数,则 的最大值为
的最大值为 B.1 C.2 D.3
B.1 C.2 D.3 上任意一点,过点P分别作双曲线的两条渐近线的垂线,垂足分别为A、B,则
上任意一点,过点P分别作双曲线的两条渐近线的垂线,垂足分别为A、B,则
 B.
B. C.
C. D.
D.
 的共轭复数是
的共轭复数是 B.
B.  C.
C.  D.
D. 
 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= . 内有零点且单调递增的是
内有零点且单调递增的是  B.
B. C.
C. D.
D.
 中,三个角
中,三个角 的对边边长分别为
的对边边长分别为 ,则
,则 的值为 .
的值为 .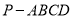 ,侧面
,侧面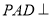 底面
底面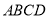 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面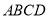 为菱形,且
为菱形,且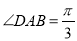 .
.
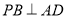 ;
;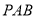 与平面
与平面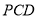 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.