题目内容
4．已知复数$z=\frac{5i}{3-4i}$（i是虚数单位），则|z|=（ ）| A． | 5 | B． | $\sqrt{5}$ | C． | $\frac{1}{5}$ | D． | 1 |
分析 利用复数代数形式的乘除运算化简，再由模的计算公式求解．
解答 解：∵$z=\frac{5i}{3-4i}$=$\frac{5i（3+4i）}{（3-4i）（3+4i）}=-\frac{4}{5}+\frac{3}{5}i$，
∴|z|=$\sqrt{（-\frac{4}{5}）^{2}+（\frac{3}{5}）^{2}}=1$．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查复数模的求法，是基础题．
练习册系列答案
相关题目
12．已知集合A={x∈z|0≤x＜3}，B={x∈R|x2≤9}，则A∩B=（ ）
| A． | {1，2} | B． | {0，1，2} | C． | {x|0≤x＜3} | D． | {x|0≤x≤3} |
12．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{a}•\overrightarrow{b}$=10，|$\overrightarrow{a}+\overrightarrow{b}$|=5$\sqrt{2}$，则|$\overrightarrow{b}$|=（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{10}$ | C． | 5 | D． | 25 |
13．已知i为虚数单位，复数z满足z-zi=1+2i，则z的共轭复数$\overline z$所对应的点位于复平面内的（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
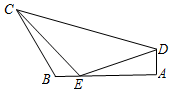如图，在平面四边形ABCD中，已知∠A=$\frac{π}{2}$，∠B=$\frac{2π}{3}$，AB=6．在AB边上取点E使得BE=1，连结EC，ED，若∠CED=$\frac{2π}{3}$，EC=$\sqrt{7}$．则CD=7．