题目内容
6．在区间[2，10]上任取一个数，这个数在区间[5，7]上的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
分析 由题意，本题符合几何概型，只要求出对应区间的长度，利用长度比得到概率值．
解答 解：由区间[2，10]的长度为8，区间[5，7]的长度为2，
则所求的概率为P=$\frac{2}{8}$=$\frac{1}{4}$．
故选：B．
点评 本题考查了几何概型概率的计算问题，是基础题目．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
17．双曲线mx2-y2=1（m∈R）与椭圆$\frac{x^2}{5}+{y^2}=1$有相同的焦点，则该双曲线的渐近线方程为（ ）
| A． | $y=±\sqrt{3}x$ | B． | $y=±\frac{{\sqrt{3}}}{3}x$ | C． | $y=±\frac{1}{3}x$ | D． | y=±3x |
1．函数f（x）=$\frac{1}{1+{x}^{2}}$的值域是（ ）
| A． | {y|y≠0} | B． | （0，1] | C． | （0，1） | D． | [1，+∞） |
18．若a＞b＞0，c＜d＜0，则一定有（ ）
| A． | ad＞bc | B． | ad＜bc | C． | ac＞bd | D． | ac＜bd |
15．若$cos（\frac{π}{2}-α）=\frac{{\sqrt{2}}}{3}$，则cos（π-2α）=（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{5}{9}$ | C． | $-\frac{2}{9}$ | D． | $-\frac{5}{9}$ |
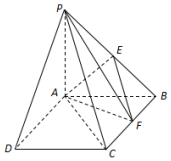如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA=AB=2，点E是PB的中点，点F在边BC上移动．