题目内容
1.已知点A(1,y1),B(9,y2)是抛物线y2=2px(p>0)上的两点,y2>y1>0,点F是它的焦点,若|BF|=5|AF|,则y12+y2的值为10.分析 由抛物线的定义:|BF|=9+$\frac{p}{2}$,|AF|=1+$\frac{p}{2}$,根据题意可知求得p,代入椭圆方程,分别求得y1,y2的值,即可求得y12+y2的值.
解答 解:抛物线y2=2px(p>0)焦点在x轴上,焦点($\frac{p}{2}$,0),
由抛物线的定义可知:|BF|=9+$\frac{p}{2}$,|AF|=1+$\frac{p}{2}$,
由|BF|=5|AF|,即9+$\frac{p}{2}$=5(1+$\frac{p}{2}$),解得:p=2,
∴抛物线y2=4x,
将A,B代入,解得:y1=2,y2=6,
∴y12+y2=10,
故答案为:10.
点评 本题考查抛物线的性质,考查抛物线方程的应用,属于中档题.

练习册系列答案
相关题目
12.经过双曲线的左焦点F1作倾斜角为30°的直线,与双曲线的右支交于点P,若以PF1为直径的圆恰好经过双曲线的右焦点,则双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
6.已知向量$\overrightarrow{a}$=(m-1,2),$\overrightarrow{b}$=(m,-3),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m等于( )
| A. | 2或-3 | B. | -2或3 | C. | $\frac{3}{5}$ | D. | 3 |
13.在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么数学就没有什么问题.”某班针对“高中生物理学习对数学的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的数学和物理成绩如表
(1)求数学成绩y对物理成绩x的线性回归方程$\widehat{y}$=$\widehat{b}$x+a($\widehat{b}$精确到0.1),若某位同学的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的五位学生中随机抽取2位参加一项知识竞赛,求选出的学生的数学成绩至少有一位高于120-分的概率.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-b$\overline{x}$)
(参考数据:902+852+742+682+632=29394)
90×130+85×125+74×110+68×95+63×90=42595)
 | 1 | 2 | 3 | 4 | 5 |
| 物理成绩 | 90 | 85 | 74 | 68 | 63 |
| 数学成绩 | 130 | 125 | 110 | 95 | 90 |
(2)要从抽取的五位学生中随机抽取2位参加一项知识竞赛,求选出的学生的数学成绩至少有一位高于120-分的概率.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-b$\overline{x}$)
(参考数据:902+852+742+682+632=29394)
90×130+85×125+74×110+68×95+63×90=42595)
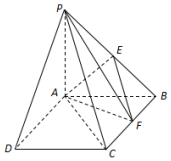 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB=2,点E是PB的中点,点F在边BC上移动.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB=2,点E是PB的中点,点F在边BC上移动.