题目内容
20.已知$C_n^0$+$2C_n^1$+${2^2}C_n^2$+…+${2^n}C_n^n$=729,则$C_n^1$++${C}_{n}^{2}$+$C_n^3$+…+${C}_{n}^{n}$的值等于63.分析 根据已知条件结合二项式定理将${C}_{n}^{0}$+2Cn1+22Cn2+…+2nCnn写成(a+b)n的形式,由此求出n的值后结合二项式系数性质公式求解即可.
解答 解:由二项式定理得(1+2)n=1•${C}_{n}^{0}$+2•Cn1+22Cn2+…+2nCnn,
所以3n=729,
解得n=6,
所以Cn0+Cn1+Cn2+…+Cnn=2n=26=64,
所以Cn1+Cn2+Cn3+…+Cnn=64-1=63.
故答案为:63.
点评 本题主要考查二项式定理展开式的逆用和二项式系数的性质公式问题,是基础题目.

练习册系列答案
相关题目
12.三次函数f(x)=x3-3x+1的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
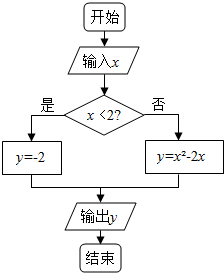 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题