题目内容
10.曲线y=$\frac{sinx}{e^x}$在点(0,0)处的切线方程为x-y=0.分析 求出曲线解析式的导函数,进而确定出点(0,0)处的切线斜率,确定出切线方程即可.
解答 解:求导得:y′=$\frac{cosx{e}^{x}-sinx{e}^{x}}{{(e}^{x})^{2}}$,
把x=0代入得:k=1,
则线y=$\frac{sinx}{e^x}$在点(0,0)处的切线方程为y=x,即x-y=0,
故答案为:x-y=0
点评 此题考查了利用导数研究曲线上某点切线方程,确定出切线方程的斜率是解本题的关键.

练习册系列答案
相关题目
15.已知$\frac{sinα-2cosα}{3sinα+5cosα}$=5,那么tanα的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{27}{14}$ | D. | -$\frac{23}{16}$ |
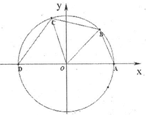 如图所示,已知点A(1,0),D(-1,0),点B,C在单位圆O上,且∠BOC=$\frac{π}{3}$.
如图所示,已知点A(1,0),D(-1,0),点B,C在单位圆O上,且∠BOC=$\frac{π}{3}$.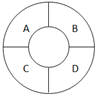 如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为84.
如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为84.