题目内容
5.已知$\overrightarrow a=(4,-2),\overrightarrow b=(cosα,sinα)$且$\overrightarrow a⊥\overrightarrow b$,则$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$为( )| A. | 2 | B. | $\frac{9}{5}$ | C. | 3 | D. | $-\frac{3}{5}$ |
分析 由$\overrightarrow a⊥\overrightarrow b$得$\overrightarrow{a}$•$\overrightarrow{b}$=0,求出sinα=2cosα,代入$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$计算即可.
解答 解:$\overrightarrow a=(4,-2),\overrightarrow b=(cosα,sinα)$,且$\overrightarrow a⊥\overrightarrow b$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=4cosα-2sinα=0,
∴sinα=2cosα,且cosα≠0;
∴$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$=$\frac{{8cos}^{3}α{+cos}^{3}α}{2cosα-cosα}$
=9cos2α
=$\frac{{9cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{{9cos}^{2}α}{{4cos}^{2}α{+cos}^{2}α}$
=$\frac{9}{5}$.
故选:B.
点评 本题考查了三角函数的化简与求值,考查了同角三角函数的基本关系式,是基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
16.已知向量$\vec a=({3,-2})$,$\vec b=({4,6})$,若向量$2\vec a+\vec b$与向量$\vec b$的夹角为θ,则cosθ=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
17.已知O为坐标原点,F是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点,A,B分别为双曲线C的左、右顶点,P为双曲线C上的一点,且PF⊥x轴,过点A的直线l与线段PF交于M,与y轴交于点E,直线BM与y轴交于点N,若|OE|=3|ON|,则双曲线C的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
14.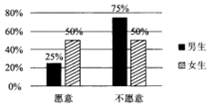 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考公式与数据:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
参考公式与数据:
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |