题目内容
17.已知O为坐标原点,F是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点,A,B分别为双曲线C的左、右顶点,P为双曲线C上的一点,且PF⊥x轴,过点A的直线l与线段PF交于M,与y轴交于点E,直线BM与y轴交于点N,若|OE|=3|ON|,则双曲线C的离心率为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 根据条件分别求出直线AE和BN的方程,求出N,E的坐标,利用|OE|=3|ON|的关系建立方程进行求解即可.
解答 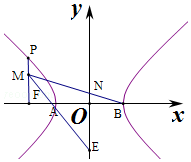 解:因为PF⊥x轴,所以设M(-c,t),
解:因为PF⊥x轴,所以设M(-c,t),
则A(-a,0),B(a,0),AE的斜率$k=\frac{t}{a-c}$,
则AE的方程为$y=\frac{t}{a-c}(x+a)$,令x=0,则$y=\frac{ta}{a-c}$,
即$E(0,\frac{ta}{a-c})$,
BN的斜率$k=-\frac{t}{a+c}$,则BN的方程为$y=-\frac{t}{a+c}(x-a)$,
令x=0,则$y=\frac{ta}{a+c}$,即$N(0,\frac{ta}{a+c})$,
因为|OE|=3|ON|,所以$3|{\frac{ta}{a+c}}|=|{\frac{ta}{a-c}}|$,即$\frac{3}{a+c}=\frac{1}{c-a}$,
则3(c-a)=a+c,即c=2a,则离心率$e=\frac{c}{a}=2$.
故选C.
点评 本题主要考查双曲线离心率的计算,根据条件求出直线方程和点N,E的坐标是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.用列举法表示集合{(x,y)|$\left\{\begin{array}{l}{y={x}^{2}}\\{y=-x}\end{array}\right.$},正确的是( )
| A. | (-1,1),(0,0) | B. | {(-1,1),(0,0)} | C. | {x=-1或0,y=1或0} | D. | {-1,0,1} |
8.命题“?x>0,x2>0”的否定是( )
| A. | ?x>0,x2<0 | B. | ?x>0,x2≤0 | C. | ?x0>0,x2<0 | D. | ?x0>0,x2≤0 |
5.已知$\overrightarrow a=(4,-2),\overrightarrow b=(cosα,sinα)$且$\overrightarrow a⊥\overrightarrow b$,则$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$为( )
| A. | 2 | B. | $\frac{9}{5}$ | C. | 3 | D. | $-\frac{3}{5}$ |
12.将函数$y=cos(2x+\frac{π}{6})$图象上的点$P(\frac{π}{4},t)$向右平移m(m>0)个单位长度得到点P',若P'位于函数y=cos2x的图象上,则( )
| A. | $t=-\frac{{\sqrt{3}}}{2}$,m的最小值为$\frac{π}{6}$ | B. | $t=-\frac{{\sqrt{3}}}{2}$,m的最小值为$\frac{π}{12}$ | ||
| C. | $t=-\frac{1}{2}$,m的最小值为$\frac{π}{6}$ | D. | $t=-\frac{1}{2}$,m的最小值为$\frac{π}{12}$ |
6.已知函数f(x)=sin2ωx-$\frac{1}{2}$(ω>0)的周期为$\frac{π}{2}$,若将其图象沿x轴向右平移a个单位(a>0),所得图象关于原点对称,则实数a的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
13.已知函数f(x)=log2(x2-ax+3a),对于任意x≥2,当△x>0时,恒有f(x+△x)>f(x),则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,2) |